Предмет: Алгебра,
автор: BackFromHell
Решите пожалуйста. Задание во вложении..
Приложения:
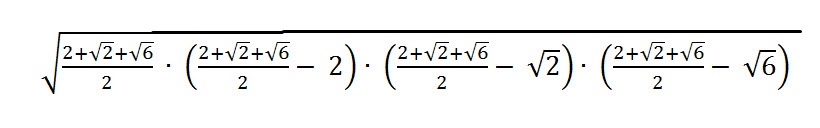
Ответы
Автор ответа:
0
первая скобка
( (2+√2+√6 ) /2 - 2 )=(2+√2+√6 - 4) / 2 = (√2+√6 -2) / 2
первая скобка и первая дробь
(2+√2+√6) / 2 * (√2+√6 -2) / 2 = ((√2+√6)^2 -2^2) / 4 =
= (2+2√12+6 -4) / 4 = (4+4√3) / 4 = 4 (1+√3) /4 =1+√3 = √3 + 1
таким же способом ТРЕТЬЯ и ЧЕТВЕРТАЯ скобки
там получается результат = √3 - 1
умножаем результаты под КОРНЕМ
√ (√3 - 1)(√3 +1) =√ (√3^2 - 1^2) = √ (3 -1) =√2
ОТВЕТ √2
( (2+√2+√6 ) /2 - 2 )=(2+√2+√6 - 4) / 2 = (√2+√6 -2) / 2
первая скобка и первая дробь
(2+√2+√6) / 2 * (√2+√6 -2) / 2 = ((√2+√6)^2 -2^2) / 4 =
= (2+2√12+6 -4) / 4 = (4+4√3) / 4 = 4 (1+√3) /4 =1+√3 = √3 + 1
таким же способом ТРЕТЬЯ и ЧЕТВЕРТАЯ скобки
там получается результат = √3 - 1
умножаем результаты под КОРНЕМ
√ (√3 - 1)(√3 +1) =√ (√3^2 - 1^2) = √ (3 -1) =√2
ОТВЕТ √2
Автор ответа:
0
Преобразуем сначала выражение под корнем.Для этого выполним действия в скобках, приведём к общему знаменателю.

А теперь по условию извлечём квадратный корень из полученного числа 2, получим .
.
А теперь по условию извлечём квадратный корень из полученного числа 2, получим
Похожие вопросы
Предмет: История,
автор: sadpm
Предмет: География,
автор: alinkamartyniyk86
Предмет: География,
автор: elinaostrovskaya97
Предмет: Обществознание,
автор: ELIA111