Предмет: Геометрия,
автор: Жориккот123
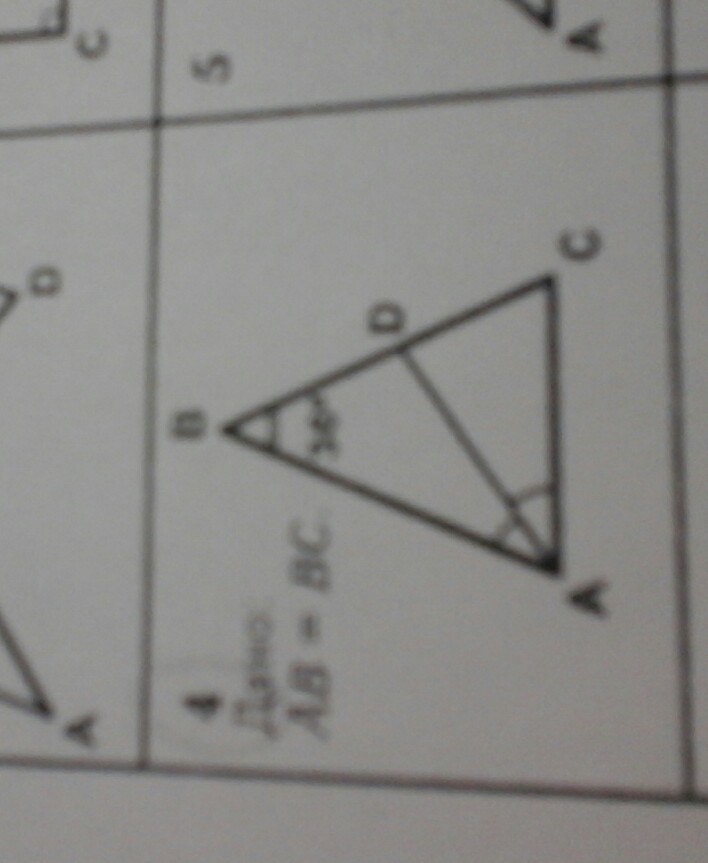
Указать подобные треугольники, доказать их подобие.
Помогите пожалуйста номер 4.
P.s на фото плохо видно угол в = 36 градусов. )
Приложения:
Ответы
Автор ответа:
0
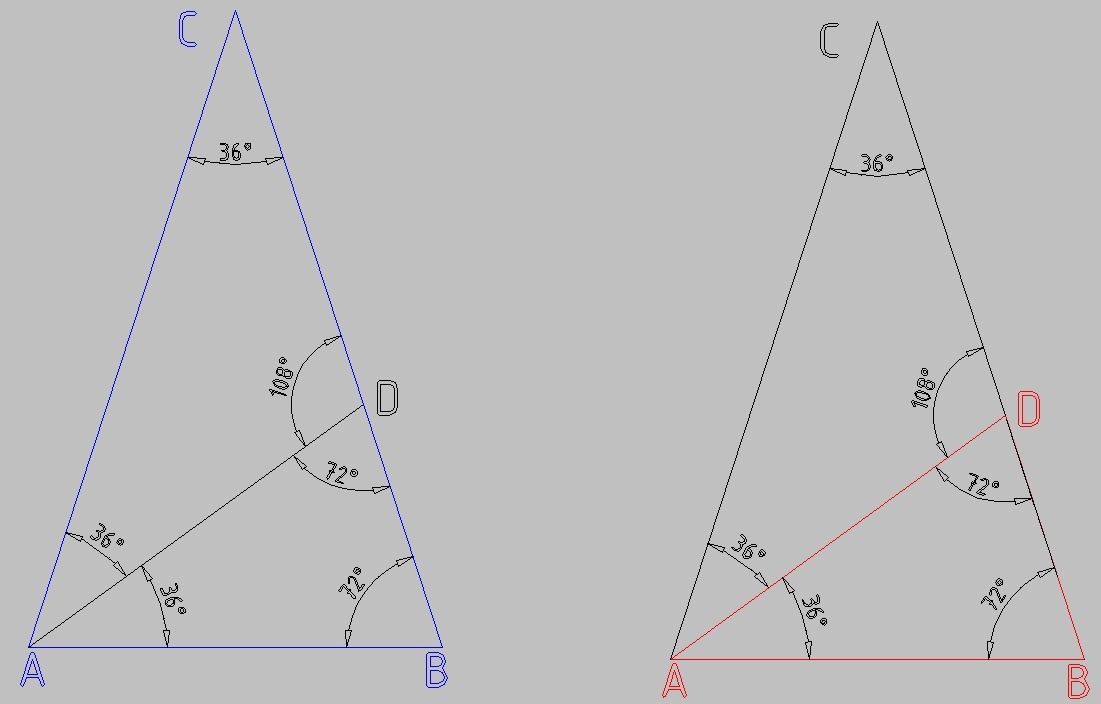
В ΔАВС
∠С = 36°
∠А = ∠В = (180-36)/2 = 72°
В ΔАВD
∠A = 72/2 = 36°
∠В = 72° из прошлого пункта
∠D = 180 - 36 - 72 = 72°
всё, подобие по трём углам
Коэффициент подобия
k = AB/AC
По теореме косинусов
AB² = АС²+BC² - 2*AC*BC*cos(36°) = 2*АС²-2*АС²*1/4(1+√5) = AC²*(2-1/2-√5/2) = AC²*1/2*(3-√5)
k = √((3-√5)/2) = √(3/2-√5/2)
некрасивый корень под корнем, немного улучшим
3/2-√5/2 = (a-b√5)² = a² - 2ab√5 + 5b²
2ab√5 = √5/2
---
ab = 1/4
a² + 5b² = 3/2
---
b = 1/(4a)
a² + 5/(4a)² = 3/2
a²+5/(16a²) = 3/2
a² = t
t² - 3/2t + 5/16 = 0
t₁ = (3/2-√(9/4-4*5/16))/2 = 3/4-1/2 = 1/4
a₁ = -1/2 - мусор
a₂ = 1/2 - это хорошо
t₂ = 3/4+1/2 = 5/4
a₃ = -√5/2 - мусор
a₄ = √5/2 - плохо
a=1/2
b = 1/(4a₂) = 1/2
k = √(3/2-√5/2) = √((a-b√5)²) = a-b√5 = 1/2-√5/2
Это золотое сечение :)
∠С = 36°
∠А = ∠В = (180-36)/2 = 72°
В ΔАВD
∠A = 72/2 = 36°
∠В = 72° из прошлого пункта
∠D = 180 - 36 - 72 = 72°
всё, подобие по трём углам
Коэффициент подобия
k = AB/AC
По теореме косинусов
AB² = АС²+BC² - 2*AC*BC*cos(36°) = 2*АС²-2*АС²*1/4(1+√5) = AC²*(2-1/2-√5/2) = AC²*1/2*(3-√5)
k = √((3-√5)/2) = √(3/2-√5/2)
некрасивый корень под корнем, немного улучшим
3/2-√5/2 = (a-b√5)² = a² - 2ab√5 + 5b²
2ab√5 = √5/2
---
ab = 1/4
a² + 5b² = 3/2
---
b = 1/(4a)
a² + 5/(4a)² = 3/2
a²+5/(16a²) = 3/2
a² = t
t² - 3/2t + 5/16 = 0
t₁ = (3/2-√(9/4-4*5/16))/2 = 3/4-1/2 = 1/4
a₁ = -1/2 - мусор
a₂ = 1/2 - это хорошо
t₂ = 3/4+1/2 = 5/4
a₃ = -√5/2 - мусор
a₄ = √5/2 - плохо
a=1/2
b = 1/(4a₂) = 1/2
k = √(3/2-√5/2) = √((a-b√5)²) = a-b√5 = 1/2-√5/2
Это золотое сечение :)
Приложения:
Похожие вопросы
Предмет: Математика,
автор: loxpyaniy
Предмет: Математика,
автор: fkuzurio
Предмет: История,
автор: marcinovskavika
Предмет: Математика,
автор: alhimag
Предмет: Геометрия,
автор: payk1