Предмет: Алгебра,
автор: Abuseebusa
70 баллов.Неопределенный интеграл(8/(x^2-2) -2/sqrt(1-4x))dx.
Пожалуйста, прошу полное решение и без ареатангенсов.
Приложения:
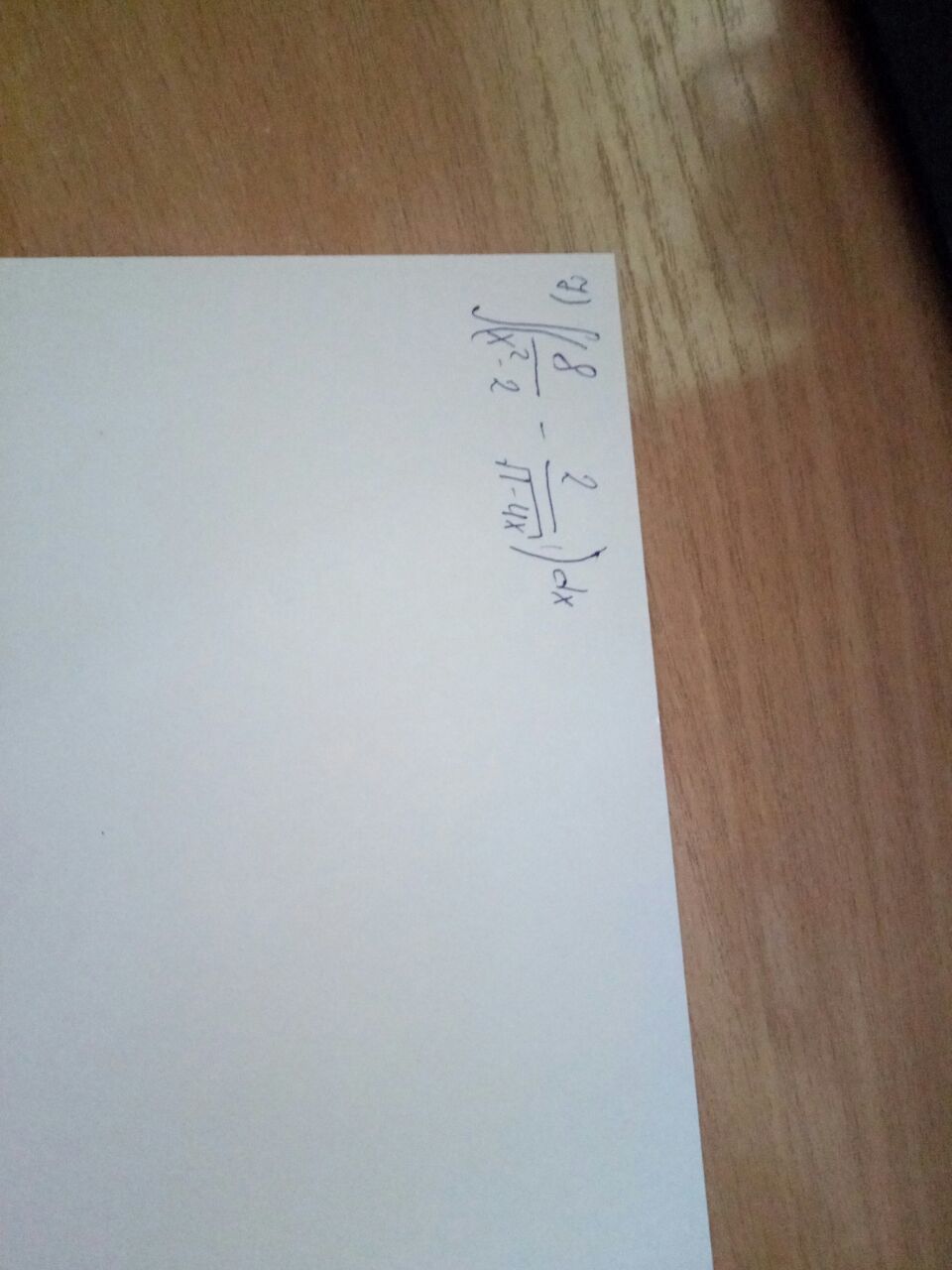
Ответы
Автор ответа:
0
Автор ответа:
0
Можно решение? Не только ответ.
Автор ответа:
0
[ln|x-√2| - ln|x+√2|]' = 1/(x-√2) - 1/(x+√2) = (x+√2)/(x^2-2) - (x-√2)/(x^2-2) = 2√2/(x^2-2)
[√(1-4x)]' = -4 / 2√(1-4x) = -2/√(1-4x)
8/(x^2-2) - 2/√(1-4x) = 2√2 * [ 2√2/(x^2-2) ] + [ -2/√(1-4x) ]
∫[ 8/(x^2-2) - 2/√(1-4x) ]dx = 2√2*[ln|x-√2| - ln|x+√2|] + √(1-4x) + C = 2√2ln( |x-√2|/|x+√2| ) + √(1-4x) + C
[√(1-4x)]' = -4 / 2√(1-4x) = -2/√(1-4x)
8/(x^2-2) - 2/√(1-4x) = 2√2 * [ 2√2/(x^2-2) ] + [ -2/√(1-4x) ]
∫[ 8/(x^2-2) - 2/√(1-4x) ]dx = 2√2*[ln|x-√2| - ln|x+√2|] + √(1-4x) + C = 2√2ln( |x-√2|/|x+√2| ) + √(1-4x) + C
Автор ответа:
0
А, там x^2 - 2. Сейчас исправлю
Автор ответа:
0
Жду.
Автор ответа:
0
Спасибо большое!
Похожие вопросы
Предмет: Физика,
автор: miroslavasemenec
Предмет: Обществознание,
автор: simonmcpe06
Предмет: Информатика,
автор: mrbob89
Предмет: Информатика,
автор: ninakek
Предмет: Литература,
автор: чек5