Предмет: Алгебра,
автор: ValeraDavay
Помогите решить уравнение( срочно)
Приложения:
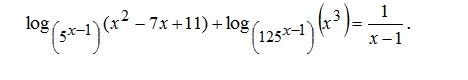
Ответы
Автор ответа:
0
Решение приложено к снимку
Приложения:

Автор ответа:
0
при условии, что x≠1, делим все на 1/(x-1)
корень x=1 - не подходит по одз, остается один: x=5
подставим его в исходное уравнение:
x=5
5^4; 25-35+11>0; 125^(-4); 5^3; 1/(5-1) - все верно, значит уравнение имеет единственный корень x=5
Ответ: x=5
Приложения:

Похожие вопросы
Предмет: Физика,
автор: Zhorchuk
Предмет: Математика,
автор: Ssssoofiia297
Предмет: Геометрия,
автор: lina171007
Предмет: Математика,
автор: Аноним