Предмет: Геометрия,
автор: feho
В прямоугольном треугольнике радиус вписанной окружности равен 1, а периметр равен 15. Найдите стороны треугольника.
Ответы
Автор ответа:
0
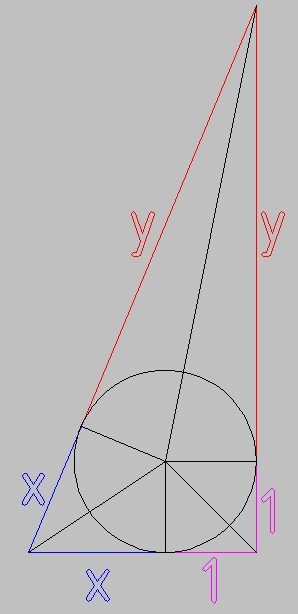
Периметр
2x+2y+2=15
x+y = 13/2
y = 13/2-x
А это теорма Пифагора
(1+x)^2+(1+y)^2=(x+y)^2
(1+x)^2+(1+13/2-x)^2=(x+13/2-x)^2
(1+x)^2+(15/2-x)^2=(13/2)^2
1+2x+x^2+225/4-15x+x^2=169/4
2x^2-13x+15 = 0
x₁ = (13-√(169-4*2*15))/(2*2) = (13-√(169-120))/4 = (13-√49)/4 = (13-7)/4 = 3/2
x₂ = (13+√(169-4*2*15))/(2*2) = (13+√(169-120))/4 = (13+√49)/4 = (13+7)/4 = 5
y₁ = 13/2-x₁ = 13/2 - 3/2 = 10/2 = 5
y₂ = 13/2-x₂ = 13/2 - 10/2 = 3/2
Решение одно, просто в нём x и y меняются местами
Теперь длины сторон
a = 1+x = 1+3/2 = 5/2
b = 1+y = 1+5 = 6
c = x+y = 3/2+5 = 13/2
2x+2y+2=15
x+y = 13/2
y = 13/2-x
А это теорма Пифагора
(1+x)^2+(1+y)^2=(x+y)^2
(1+x)^2+(1+13/2-x)^2=(x+13/2-x)^2
(1+x)^2+(15/2-x)^2=(13/2)^2
1+2x+x^2+225/4-15x+x^2=169/4
2x^2-13x+15 = 0
x₁ = (13-√(169-4*2*15))/(2*2) = (13-√(169-120))/4 = (13-√49)/4 = (13-7)/4 = 3/2
x₂ = (13+√(169-4*2*15))/(2*2) = (13+√(169-120))/4 = (13+√49)/4 = (13+7)/4 = 5
y₁ = 13/2-x₁ = 13/2 - 3/2 = 10/2 = 5
y₂ = 13/2-x₂ = 13/2 - 10/2 = 3/2
Решение одно, просто в нём x и y меняются местами
Теперь длины сторон
a = 1+x = 1+3/2 = 5/2
b = 1+y = 1+5 = 6
c = x+y = 3/2+5 = 13/2
Приложения:
Похожие вопросы
Предмет: Физкультура и спорт,
автор: Kristina9999999999
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: aneliaakopan62
Предмет: Математика,
автор: SoFkA12004
Предмет: Математика,
автор: lena7k