Question

Номер 2.60. Именно нужно доказательство, не надо за место х ставить числа. Спасибо, что внимательно прочитали!

Answer 1

x⁴ − 3x³ + 4x² − x + 2 = 0
(x⁴ + 4x² + 2) − (3x³ + x) =  0
x⁴ + 4x² + 2 = 3x³ + x
x⁴ + 4x² + 2 = x(3x² + 1)

x⁴ + 4x² ≥0      ⇒       x⁴ + 4x² +2 ≥ 2
3x² ≥ 0           ⇒        3x² + 1 ≥  1

x⁴ + 4x² + 2 = x(3x² + 1)
Слева стоит число положительное
Справа в скобке - число положительное
⇒ чтобы справа произведение оставалось положительным, x должен быть положительным.

(+) = x * (+)        ⇒    x > 0

Ответ: отрицательного корня быть не может

Answer 2

наука показывает, что нет ни одного действительного. Все четыре - мнимые.

Answer 3

Это программа 7 класса, умножение многочленов, о каких мнимых корнях речь?

Answer 4

А действительных корней нет, потому что (+)слева не может быть равен 0*(+)

Answer 5

Разложение на множители наверно. НЕ УБЕДИЛИ. Корней нет - ни положительных, ни отрицательных.

Answer 6

Да, это тема многочленов и разложения на множители в ШКОЛЬНОЙ программе (не вузовской), поэтому мой ответ на уровне 7 класса, комплексных чисел там еще точно не изучают

Answer 7

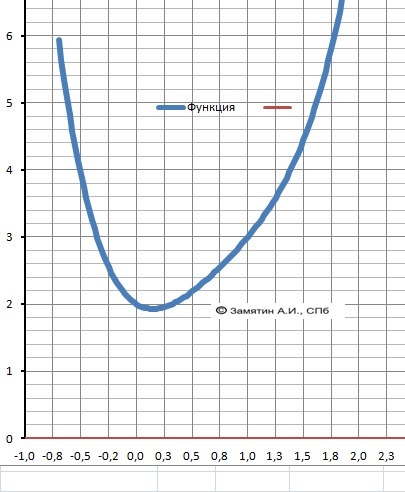
У этой функции вообще нет действительных корней.
Все четыре корня у неё мнимые.
График функции в приложении.
Корней функции - пересечения с осью Х - нет.