Предмет: Алгебра,
автор: alexey385p29tn8
помогите ,пожалуйста ,решить уравнение
Приложения:
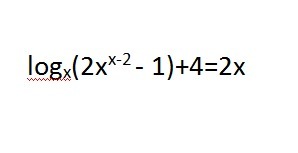
Ответы
Автор ответа:
0
основание логарифма х>0 и x≠1 (это ОДЗ)
logₓ(2*x⁽ˣ⁻²⁾-1) = 2*x - 4
2*x⁽ˣ⁻²⁾-1 = x⁽²ˣ⁻⁴⁾
замена: x⁽ˣ⁻²⁾ = t
2*t - 1 = t²
t² - 2t + 1 = 0
(t - 1)² = 0 ---> t = 1
x⁽ˣ⁻²⁾ = 1 (1 = x⁰)
x-2 = 0
x = 2
и можно сделать проверку: log₂(2*2⁰ - 1)+4 = 2*2
log₂(1)+4 = 4
0+4 = 4
logₓ(2*x⁽ˣ⁻²⁾-1) = 2*x - 4
2*x⁽ˣ⁻²⁾-1 = x⁽²ˣ⁻⁴⁾
замена: x⁽ˣ⁻²⁾ = t
2*t - 1 = t²
t² - 2t + 1 = 0
(t - 1)² = 0 ---> t = 1
x⁽ˣ⁻²⁾ = 1 (1 = x⁰)
x-2 = 0
x = 2
и можно сделать проверку: log₂(2*2⁰ - 1)+4 = 2*2
log₂(1)+4 = 4
0+4 = 4
Похожие вопросы
Предмет: География,
автор: dvs2504
Предмет: Химия,
автор: Fortnat
Предмет: Литература,
автор: rozkovmihail
Предмет: Химия,
автор: ЕркебуланМанкеев