Question

Пожалуйста подробно)
Решить неравенство$log frac{2}{2} x-3 log_{2}x leq 4$

Answer 1

$log^2_2x - 3 log_2x leq 4 \ \ log^2_2x - 3log_2x-4 leq 0$

t = log₂x
t² - 3t - 4 ≤ 0
(t - 4)(t + 1) ≤ 0

Метод интервалов.
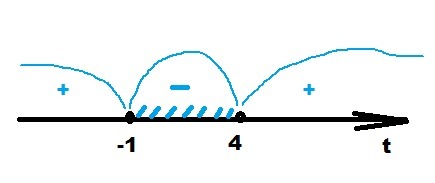
На числовой оси отметить точки t₁ = -1 и t₂ = 4
Проверить полученные 3 интервала на знак +/- (см. рисунок)

-1 ≤ t ≤ 4
-1 ≤ log₂x ≤ 4
$-log_22 leq log_2x leq 4log_22 \ \ log_2 frac{1}{2} leq log_2x leq log_216$

$frac{1}{2} leq x leq 16$
ОДЗ:  x > 0

Ответ: x ∈ [$frac{1}{2} ;$16]