Предмет: Геометрия,
автор: NataGokh
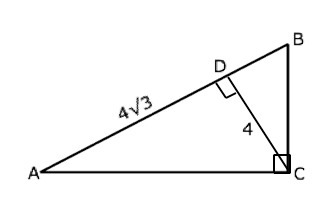
высота CD прямоугольного треугольника АВС, проведённая из вершины прямого угла, равна 4 см. Известно что она делит гипотенузу на отрезки ,один из которых равен 4 корней из 3 см. Найдите градусные меры острых углов треугольника АВС.
Ответы
Автор ответа:
0
Пусть AD = 4 * корень(3). Треугольник CDA прямоугольный, поэтому tg(CAD) = CD / DA = 4 / (4 * корень(3)) = 1 / корень(3) CAD = 30 градусов. Углы треугольника ABC: CAB + ABC + BCA = 180 30 + ABC + 90 = 180 ABC = 180 - 30 - 90 = 60 Ответ: 30 градусов и 60 градусов.
Автор ответа:
0
Вариант решения.
Найдем второй отрезок гипотенузы.
Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное для отрезков, на которые делится гипотенуза этой высотой.⇒
СD²=АD•ВD
16=4√3•BD
BD=16:4√3=
Из ∆ АВD: ∠САD= arctg , т.е. 30°
Из ∆ ВСD ∠СВD=arctg , т.е.60°
Приложения:
Похожие вопросы
Предмет: Українська мова,
автор: Аноним
Предмет: Литература,
автор: kamilaasankulova5
Предмет: Литература,
автор: 1234563434343
Предмет: Алгебра,
автор: Аноним
Предмет: Математика,
автор: сергеевнаполина