Question

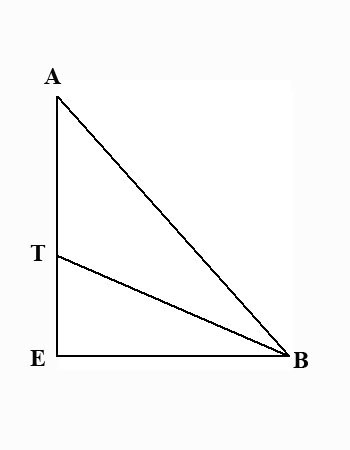
В прямоугольном треугольнике АВЕ с прямым углом Е проведена биссектриса ВТ, причем АТ = 15, ТЕ = 12. Найдите площадь треугольника АВТ

Answer 1

Дано: прямоугольный треугольник ABE, ∠AEB = 90°, AT = 15, TE = 12.
Найти: площадь треугольника ΔABT.
Решение:
(см. также рисунок)
Высота AE = AT + TE = 15 + 12 = 27 известна. Надо найти основание ЕВ. Для этого воспользуемся свойством биссектрисы. Биссектриса делит противоположную сторону на части, пропорциональные прилегающим сторонам:
$frac{ET}{AT} = frac{EB}{AB} \ \ frac{EB}{AB} = frac{12}{15}$
$AB = frac{15}{12} EB$
По теореме Пифагора:
$AB^2 = AE^2 + EB^2 = 27^2 + EB^2$
$frac{15^2}{12^2} EB^2 = 27^2 + EB^2 \ \ frac{15^2}{12^2} EB^2 - EB^2 = 27^2 \ \ EB^2 (frac{15^2}{12^2} - 1) = 27^2 \ \ EB^2 frac{15^2 - 12^2}{12^2} = 27^2 \ \ EB * frac{ sqrt{15^2 - 12^2} }{12} = 27 \ \ EB = frac{27*12}{ sqrt{(15-12)*(15+12)} } = frac{27*12}{ sqrt{3*27} } = frac{27*12}{9} =36$
Площадь треугольника ΔABE равна:
$S_{Delta ABE} = frac{1}{2} *AE * EB = frac{1}{2} *27 * 36 = 486$
Площадь треугольника ΔTBE равна:
$S_{Delta TBE} = frac{1}{2} *TE * EB = frac{1}{2} *12 * 36 = 216$
Площадь треугольника ΔABT равна:
$S_{Delta ABT} = S_{Delta ABE} - S_{Delta TBE} = 486 - 216 = 270$

Ответ: 270