Предмет: Математика,
автор: Mariia56
Помогите,пожалуйста,с высшей математикой.
Приложения:
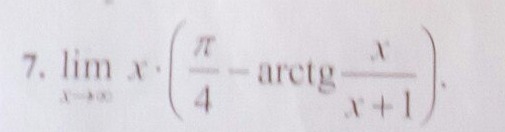
Ответы
Автор ответа:
0
Найти предел

Решение
![lim_{x to infty}xcdot( frac{pi}{4}-arctg( frac{x}{x+1}) )=[0cdot infty] lim_{x to infty}xcdot( frac{pi}{4}-arctg( frac{x}{x+1}) )=[0cdot infty]](https://tex.z-dn.net/?f=+lim_%7Bx+to+infty%7Dxcdot%28+frac%7Bpi%7D%7B4%7D-arctg%28+frac%7Bx%7D%7Bx%2B1%7D%29++%29%3D%5B0cdot++infty%5D+)
Данную неопределенность необходимо привести к виду 0/0 и применить правило Лопиталя





Поэтому

Ответ 0,5
Решение
Данную неопределенность необходимо привести к виду 0/0 и применить правило Лопиталя
Поэтому
Ответ 0,5
Похожие вопросы
Предмет: Химия,
автор: AXCACAA
Предмет: Английский язык,
автор: monosovserzat
Предмет: Физика,
автор: nazgul12345678
Предмет: Математика,
автор: никита200414
Предмет: Математика,
автор: кянан1