Предмет: Алгебра,
автор: Olga130600
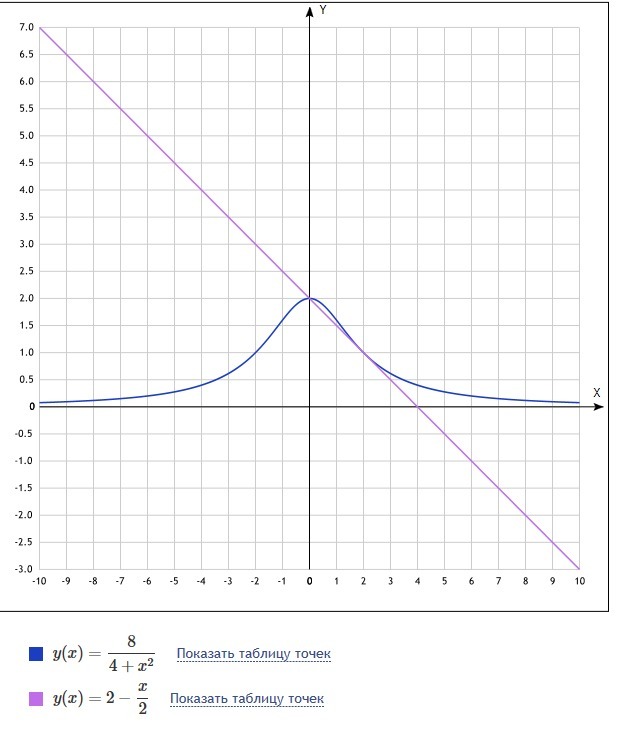
Найти уравнение касательной к графику функции y=8/(4+x^2) в точке с абсциссой x=2
Ответы
Автор ответа:
0
уравнение касательной в точке х0
g(x0)=y(x0)+y`(x0)(x-x0)
y(x0)=y(2)=8/(4+4)=1
y`=-8*2x/(4+x^2)^2
y`(2)=-32/64=-1/2
g(x)=1+(-1/2)(x-2)=1-(x-2)/2=2-x/2-уравнение касательной
g(x0)=y(x0)+y`(x0)(x-x0)
y(x0)=y(2)=8/(4+4)=1
y`=-8*2x/(4+x^2)^2
y`(2)=-32/64=-1/2
g(x)=1+(-1/2)(x-2)=1-(x-2)/2=2-x/2-уравнение касательной
Приложения:
Похожие вопросы
Предмет: Українська мова,
автор: irakutniv
Предмет: Алгебра,
автор: hryhorchukdasha
Предмет: Русский язык,
автор: hepefor833
Предмет: Математика,
автор: Can4eck0
Предмет: Обществознание,
автор: VELIKAYA11