Предмет: Математика,
автор: myslim0717
решить дефференциальное уравнение (2x-1)dy=(y+1)dx и найти его частное решение, удовлетворяющее: при x=5 y=5
Приложения:
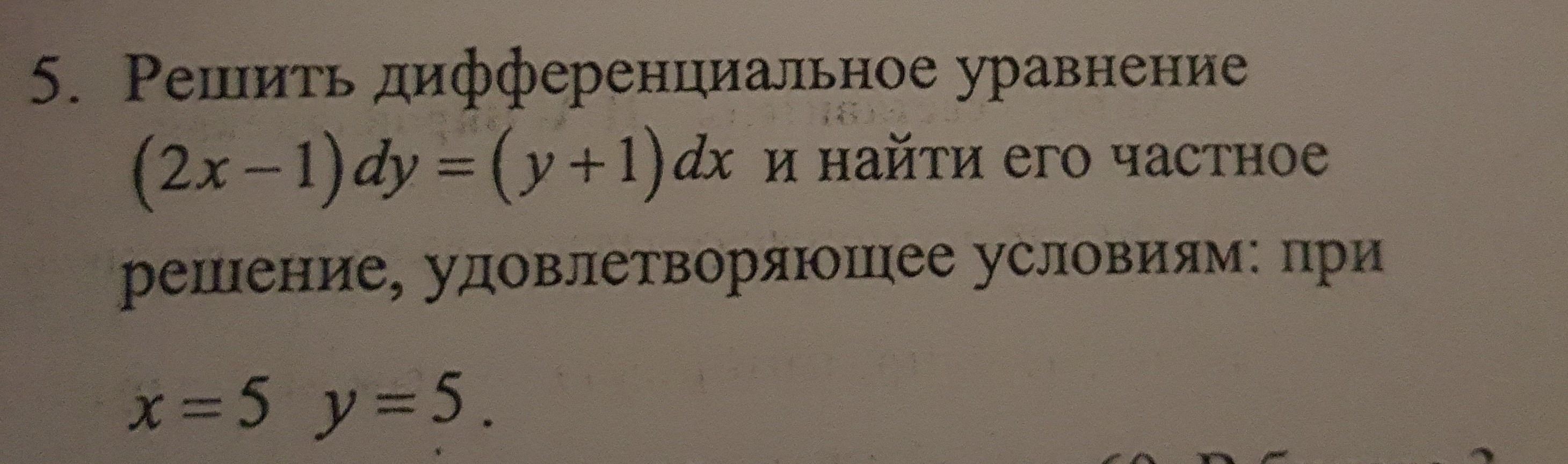
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Английский язык,
автор: nejmark26
Предмет: Математика,
автор: Jama2006f
Предмет: Математика,
автор: toyirjonovashakhrizo
Предмет: Геометрия,
автор: 1113356