Предмет: Математика,
автор: iriha777
Найдите область определения функции.
Приложения:
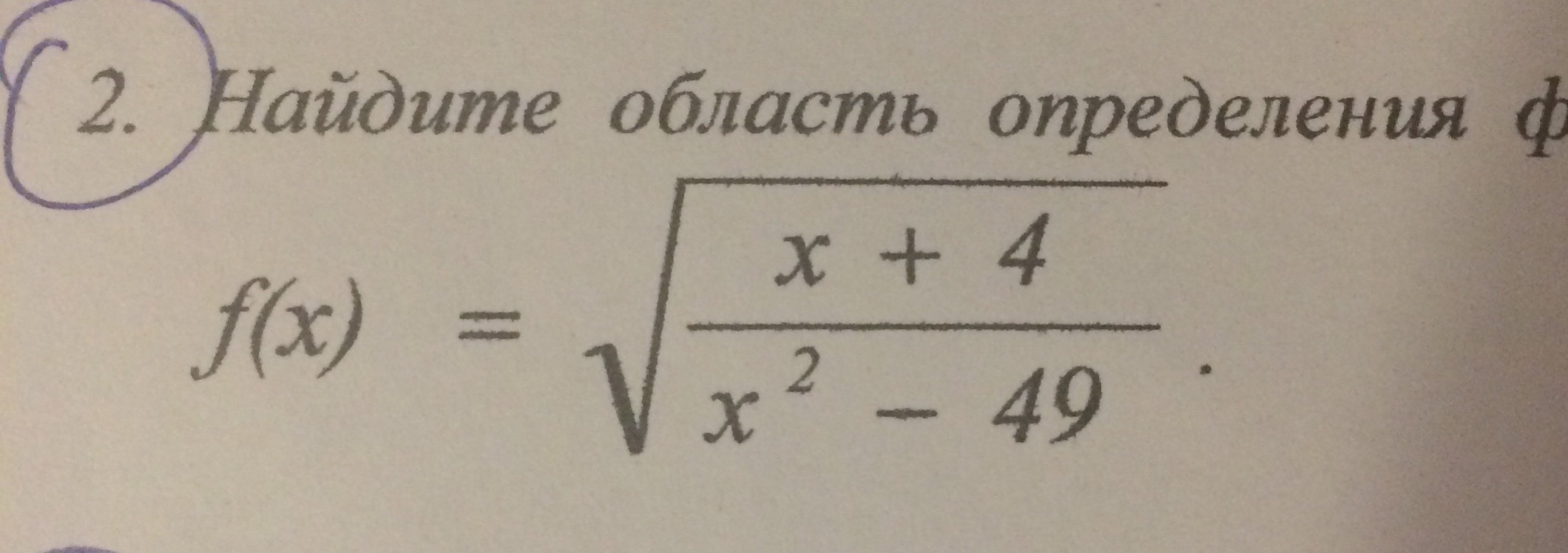
Ответы
Автор ответа:
0
Решение:

Функция имеет смысл, если x² - 49 ≠ 0 (делить на 0 нельзя) и если ≥ 0 (вынести корень из отрицательного числа нельзя)
≥ 0 (вынести корень из отрицательного числа нельзя)
На основе этих неравенств составим и решим систему, второе уравнение которого заменив равносильным

1: x² - 49 ≠ 0
x² ≠ 49
x ≠ 7
x ≠ -7
x ∈ (-∞;-7) ∪ (-7;7) ∪ (7;∞)
2: (x + 4)(x² - 49) ≥ 0
Приведем к виду 1 и решим методом интервала
(x + 4)(x - 7)(x + 7) ≥ 0
1) f(x) = (x + 4)(x - 7)(x + 7)
2) f(x) = 0, если x = -4; x = 7; x = -7 (произведение равно нулю тогда и только тогда, когда хоть один из множителей равен нулю)
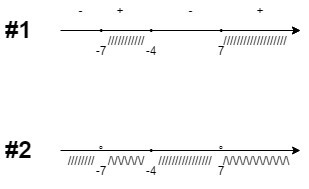
3) [график в приложении под номером 1]
x ∈ [-7;-4] ∪ [7;∞)
Найдем пересечение неравенств [В приложении под номером 2]
 или
или 
D(y)
= (-7 ; -4] ∪ (7 ; ∞)
Функция имеет смысл, если x² - 49 ≠ 0 (делить на 0 нельзя) и если
На основе этих неравенств составим и решим систему, второе уравнение которого заменив равносильным
1: x² - 49 ≠ 0
x² ≠ 49
x ≠ 7
x ≠ -7
x ∈ (-∞;-7) ∪ (-7;7) ∪ (7;∞)
2: (x + 4)(x² - 49) ≥ 0
Приведем к виду 1 и решим методом интервала
(x + 4)(x - 7)(x + 7) ≥ 0
1) f(x) = (x + 4)(x - 7)(x + 7)
2) f(x) = 0, если x = -4; x = 7; x = -7 (произведение равно нулю тогда и только тогда, когда хоть один из множителей равен нулю)
3) [график в приложении под номером 1]
x ∈ [-7;-4] ∪ [7;∞)
Найдем пересечение неравенств [В приложении под номером 2]
D(y)
= (-7 ; -4] ∪ (7 ; ∞)
Приложения:
Автор ответа:
0
Обратите внимание, что это поле для решения и объяснений, а не только для ответов.
Похожие вопросы
Предмет: Українська література,
автор: playmonster280
Предмет: Українська мова,
автор: maksumdenisenko93
Предмет: Математика,
автор: tehelpplls
Предмет: Математика,
автор: ТатьянаГашук
Предмет: Математика,
автор: darsnukaeva2