Question

Помогите мне пожалуйста!!!!!

Точки А и В лежат на окружности одного основания цилиндра, а точки С и D– на окружности другого основания цилиндра, причем ABCD – квадрат. Найти высоту цилиндра, если известно, что радиус основания цилиндра равен 6, а диагональ квадрата равна 13.

Answer 1

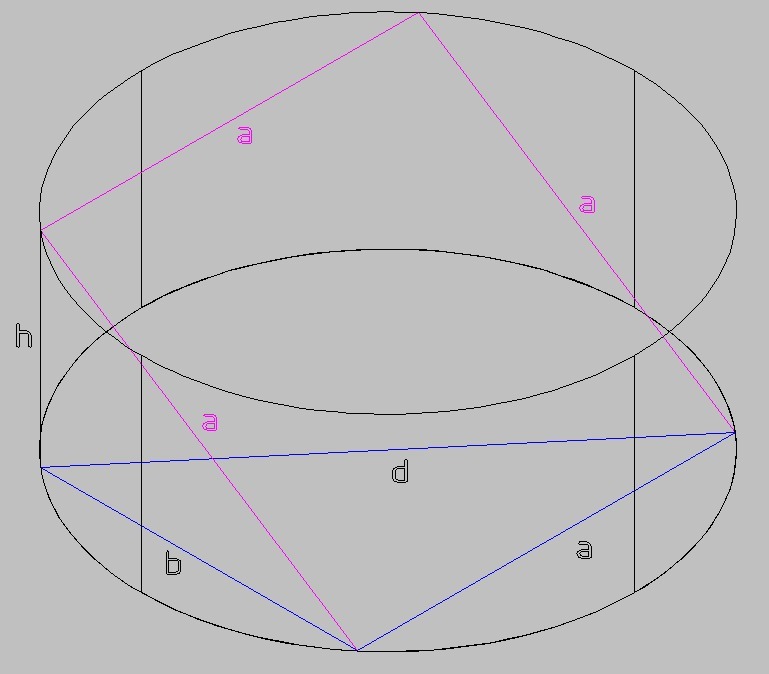
Если диагональ квадрата равна 12, то сторона квадрата
a = 13/√2 ≈ 9,19
меньше диаметра цилиндра, равного
d = 6*2 = 12.
И возможны два варианта размещения квадрата в цилиндре -
а) тривиальный. Квадрат вертикален, его плоскость параллельна оси цилиндра. Высота цилиндра равна стороне квадрата,
h = 13/√2
б) наклонный, центр квадрата совпадает с центром цилиндра
На рисунке проекция квадрата на основание - синяя
b - проекция наклонной стороны квадрата на плоскость основания
По Пифагору:
a² + b² = d²
b² = 12²- (13/√2)² = 12² - 13²/2 = 144 - 169/2 = 119/2
b = √(119/2)
И теперь ещё раз по теореме Пифагора, но уже для вертикально расположенного прямоугольного треугольника
h² + b² = a²
h² = a² - b² = (13/√2)² - (√(119/2))² = 169/2 - 119/2 = 50/2 = 25
h = √25 = 5
И это ответ :)