Предмет: Алгебра,
автор: prestigpad
найдите точку максимума функции y=x^3-7x^2+15x-22
Ответы
Автор ответа:
0
Дана функция y = x³ - 7x² + 15x - 22.
Производная равна:
y' = 3x² - 14x + 15.
Приравниваем её нулю:
3x² - 14x + 15 = 0.
Квадратное уравнение, решаем относительно x: Ищем дискриминант:
D=(-14)^2-4*3*15=196-4*3*15=196-12*15=196-180=16;Дискриминант больше 0, уравнение имеет 2 корня:
x_1 = (√16-(-14))/(2*3) = (4-(-14))/(2*3) = (4+14)/(2*3) = 18/(2*3) = 18/6 = 3;x_2 = (-√16-(-14))/(2*3) = (-4-(-14))/(2*3) = (-4+14)/(2*3) = 10/(2*3) = 10/6 = 5/3 ≈ 1.666667.
Имеем 2 критические точки и 3 промежутка.
На промежутках находят знаки производной. Где производная положительна - функция возрастает, где отрицательна - там убывает. Точки, в которых происходит смена знака и есть точки экстремума - где производная с плюса меняется на минус - точка максимума, а где с минуса на плюс - точки минимума.
x = 0 1,666667 2 3 4
y' = 15 0 -1 0 7.
Отсюда выводы:
- функция возрастает на промежутках (-∞; (2/3) и (3; +∞),
- функция убывает на промежутке ((2/3); 3),
- максимум в точке х =(2/3),
- минимум в точке х = 3,
Производная равна:
y' = 3x² - 14x + 15.
Приравниваем её нулю:
3x² - 14x + 15 = 0.
Квадратное уравнение, решаем относительно x: Ищем дискриминант:
D=(-14)^2-4*3*15=196-4*3*15=196-12*15=196-180=16;Дискриминант больше 0, уравнение имеет 2 корня:
x_1 = (√16-(-14))/(2*3) = (4-(-14))/(2*3) = (4+14)/(2*3) = 18/(2*3) = 18/6 = 3;x_2 = (-√16-(-14))/(2*3) = (-4-(-14))/(2*3) = (-4+14)/(2*3) = 10/(2*3) = 10/6 = 5/3 ≈ 1.666667.
Имеем 2 критические точки и 3 промежутка.
На промежутках находят знаки производной. Где производная положительна - функция возрастает, где отрицательна - там убывает. Точки, в которых происходит смена знака и есть точки экстремума - где производная с плюса меняется на минус - точка максимума, а где с минуса на плюс - точки минимума.
x = 0 1,666667 2 3 4
y' = 15 0 -1 0 7.
Отсюда выводы:
- функция возрастает на промежутках (-∞; (2/3) и (3; +∞),
- функция убывает на промежутке ((2/3); 3),
- максимум в точке х =(2/3),
- минимум в точке х = 3,
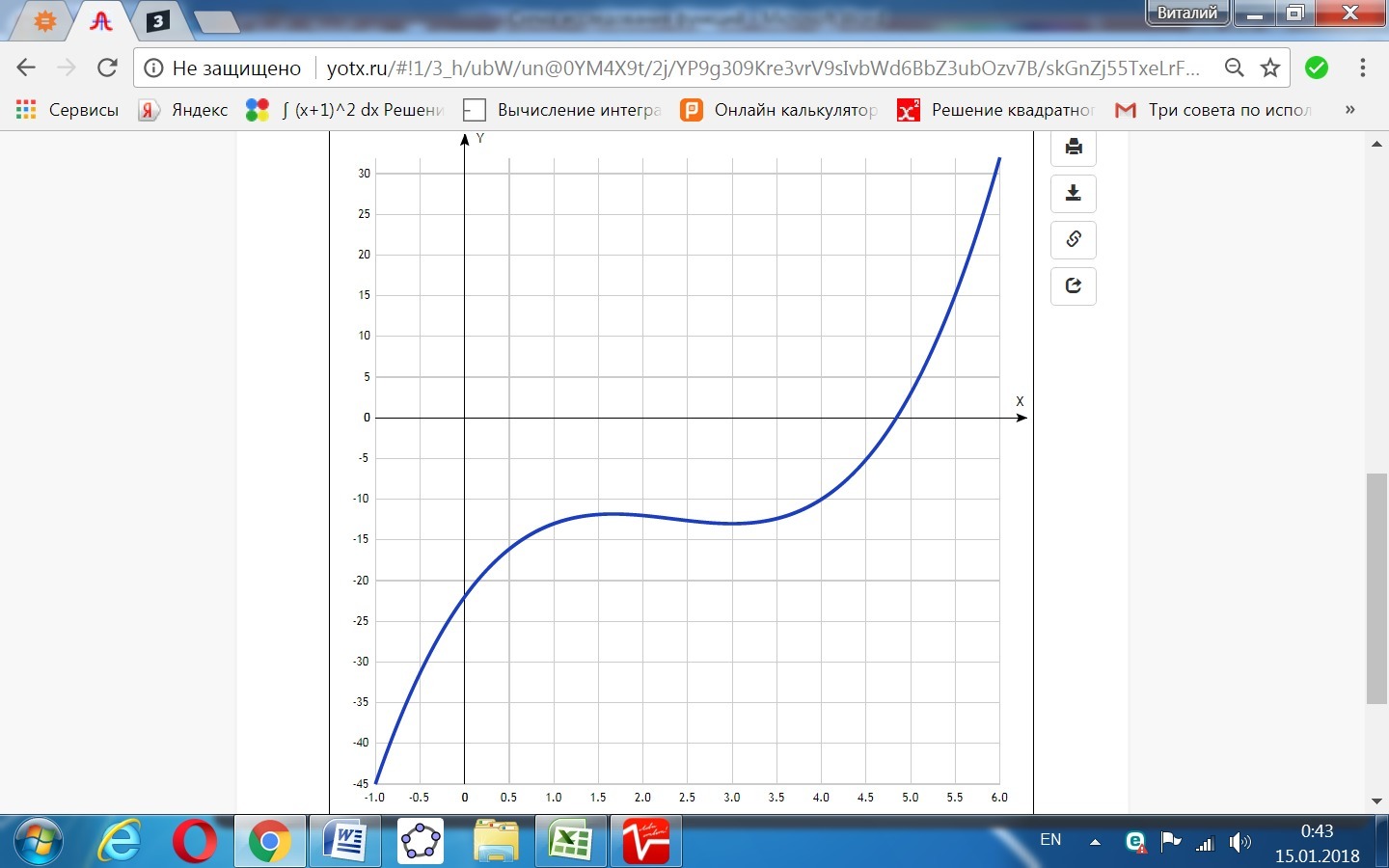
Приложения:
Похожие вопросы
Предмет: Алгебра,
автор: nastgraff
Предмет: Математика,
автор: shiavanikashi
Предмет: Биология,
автор: kiruhinkiruhin87
Предмет: Математика,
автор: maks3754128maks
Предмет: Математика,
автор: gulmirarakhmtu