Предмет: Алгебра,
автор: Cu6upb9lk
25 баллов. Алгебра 10 класс
Приложения:
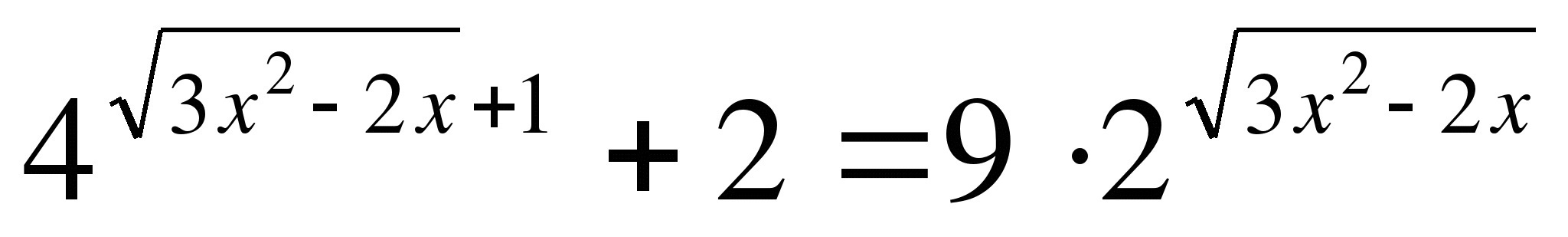
Ответы
Автор ответа:
0
делаем замену:

тогда:

обратная замена:

Ответ: x1=1; x2=-1/3
тогда:
обратная замена:
Ответ: x1=1; x2=-1/3
Автор ответа:
0
обновите страницу
Автор ответа:
0
теперь нормально
Автор ответа:
0
почему 3x^2 - 2x больше о? и как ты извлёк его из корня?
Автор ответа:
0
так, это выражение равно 1, а следовательно больше либо равно 0?
Автор ответа:
0
возвел обе части в квадрат
Автор ответа:
0
подкоренное выражение всегда неотрицательно, поэтому
положим, что
возвращаемся к обратной замене:
1.
решений нет
2.
ОТВЕТ:
Похожие вопросы
Предмет: Українська мова,
автор: gostuknela
Предмет: Русский язык,
автор: moiseevanastya221019
Предмет: Информатика,
автор: ichikvani
Предмет: Математика,
автор: Анастапсия