Question

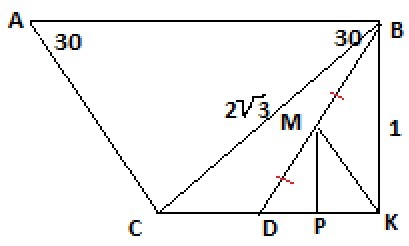
В равнобедренной трапеции АВСD(АВ||СD), угол А равен 30 градусов, высота ВК равна 1см, сторона ВС равна 2^3 см.Найдите площадь треугольника МКD, где М - середина отрезка ВD

Answer 1

∠ABD=∠A=30° -по условию, как углы в основании равнобедренной трапеции.  ∠DBK=90-∠ABD=60°, значит ∠BDK=30°⇒
DB=1*2=2см, так как катет BK, лежащий против угла в 30°, равен половине гипотенузы.
MD=MB, MD=1/2DB=1/2*2=1см
DK=√(DB²-BK²)=√(4-1)=√3
MP лежит против  ∠MDK=30°⇒
MP=1/2MD=1/2,  площадь MDK =MP*1/2DK=1/4√3
Ответ:S=1/4√3