Предмет: Математика,
автор: pochtichudo
Помогите найти производные функций при заданном значении аргумента.
Приложения:
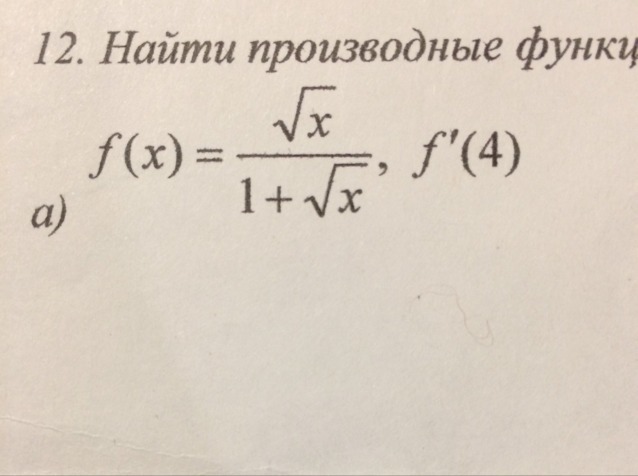
Ответы
Автор ответа:
0
найти производные функций при заданном значении аргумента f'(4)

Решение
Найдем производную как производную дроби


Найдем значение производной при х = 4

Ответ: f'(4) = 1/36
Решение
Найдем производную как производную дроби
Найдем значение производной при х = 4
Ответ: f'(4) = 1/36
Похожие вопросы
Предмет: Математика,
автор: Аноним
Предмет: Русский язык,
автор: 28371947
Предмет: Право,
автор: Nikita35209
Предмет: Математика,
автор: rakuwa87
Предмет: Математика,
автор: Аноним