Question

Найдите наибольшее значение функции у=х^3-6х^2 на отрезаешь [-3;3]

Answer 1

ДАНО
y = x³ - 6*x² = x²*(x-6)
D(x)∈[-3;3]
НАЙТИ
Экстремумы функции.
РЕШЕНИЕ
Найдем экстремумы функции - они могут быть внутри области определения.
y'(x) = 3x²-12x = 3*x*(x-4)
Экстремум при х =0 и у(0) = 0 - максимальное значение.
Минимальное значение при Х = - 3.
Вычисляем значение 
y(-3) = -27 - 6*9 = - 81.
ОТВЕТ E(y) ∈[-81;0] - область значений.
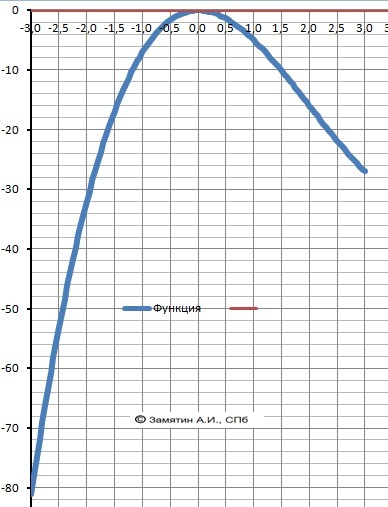
График функции - в приложении - подарок.