Предмет: Математика,
автор: renata777renatp0sxrh
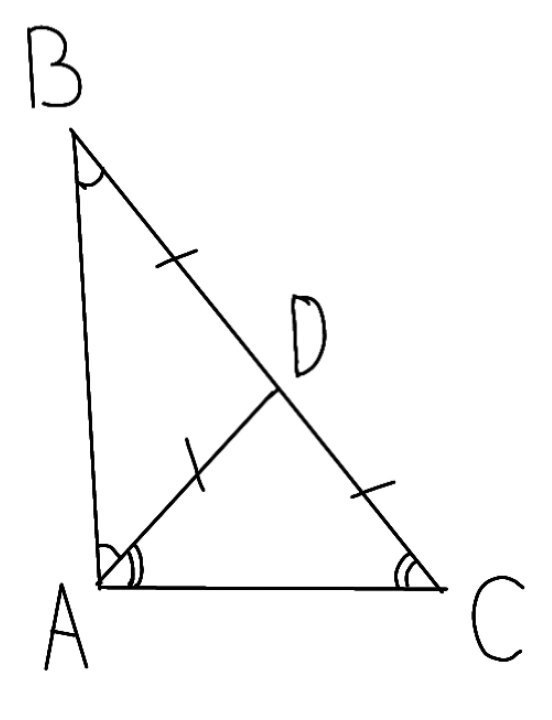
В треугольнике АВС АD медиана равна половине стороны ВС. Докажите, что треугольник АВС прямоугольный
Ответы
Автор ответа:
0
Т.к AD - медиана, то BD=DC=0.5 от BC (половина стороны)
По условию AD=BD=DC, то треугольник ABD и ADC равнобедренные.
Значит угол DCA=DAC, BAD=ABD.
Поскольку во всех треугольниках сумма углов равна 180°, то
DCA+DAC+BAD+ABD=180°, т.к DCA=DAC, BAD=ABD, то
2DAC+2BAD=180°
2*(DAC+BAD)=180
DAC+BAD=90°.
=> треугольник ABC прямоугольный.
По условию AD=BD=DC, то треугольник ABD и ADC равнобедренные.
Значит угол DCA=DAC, BAD=ABD.
Поскольку во всех треугольниках сумма углов равна 180°, то
DCA+DAC+BAD+ABD=180°, т.к DCA=DAC, BAD=ABD, то
2DAC+2BAD=180°
2*(DAC+BAD)=180
DAC+BAD=90°.
=> треугольник ABC прямоугольный.
Приложения:
Похожие вопросы
Предмет: Математика,
автор: 894655
Предмет: Другие предметы,
автор: Aylainkognito
Предмет: Химия,
автор: pikadarina11
Предмет: Алгебра,
автор: Zeus12345
Предмет: Математика,
автор: blondinochcka