Question

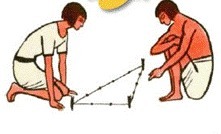
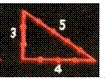
Древние египтяне могли отмерять прямые углы в полях, зная о соотношении сторон в прямоугольном треугольнике. Нам это соотношение известно в виде теоремы Пифагора: сумма квадратов катетов равна квадрату гипотенузы. Для этого они брали длинную веревку, делили ее на 12 равных отрезков и составляли из нее прямоугольный треугольник со сторонами 3, 4 и 5 отрезков. Угол между сторонами в 3 и 4 отрезков получался прямым. Но в полях возникает практическая проблема. Как разделить веревку на 12 равных отрезков? При этом хотя бы одна из сторон треугольника должна совпадать по размеру с фактической длиной или шириной поля. Вопрос: какова длина отрезка, с которого египтяне начинали измерение? Введите только число.

Answer 1

По условию хотя бы одна из сторон треугольника должна совпадать по размеру с фактической длиной или шириной поля. Пусть это будет ширина поля. Тогда вдоль ширины поля кладём веревку.

 |_________|__________|__________|___________| 

Длину этой верёвки делим узелками на 4 равных отрезка (для этого веревка складывается вдвое, потом еще вдвое).

 Далее удлиним верёвку, отмерив на ней ещё 2 раза ширину поля, и получим, наконец, верёвку, содержащую три ширины поля.

 В  верёвке, содержащей три ширины поля, будет 12 равных отрезков, которые получим с помощью складывания вдвое и ещё вдвое и обозначим их узелками.