Предмет: Математика,
автор: karenpetrosyan
Найти угол между прямыми (x-1)/2 = (y+2)/-1 = z/-2 и (x+1)/1 = (y+11)/2 = (z+6)/1
и выяснить расположение прямых
Приложения:
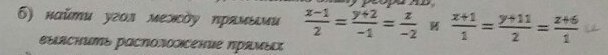
Ответы
Автор ответа:
0
Две прямые лежат в одной плоскости, если смешанное произведение их направляющих векторов и третьего вектора, проведённого между двумя точками, лежащими на этих прямых, равно 0 . (При равенстве нулю смешанного произведения делаем вывод о компланарности трёх векторов.)
Из уравнения прямых можно выписать координаты направляющих векторов и координаты точек, лежащих на прямых .

Прямые лежат в одной плоскости.
Найдём угол между прямыми.

Из уравнения прямых можно выписать координаты направляющих векторов и координаты точек, лежащих на прямых .
Прямые лежат в одной плоскости.
Найдём угол между прямыми.
Автор ответа:
0
Спасибо огромное
Похожие вопросы
Предмет: Русский язык,
автор: LIRIKOT
Предмет: Математика,
автор: kkarimova21
Предмет: Геометрия,
автор: yakubovychtaras
Предмет: Математика,
автор: lulopik
Предмет: Математика,
автор: ЖанараНяша