Question

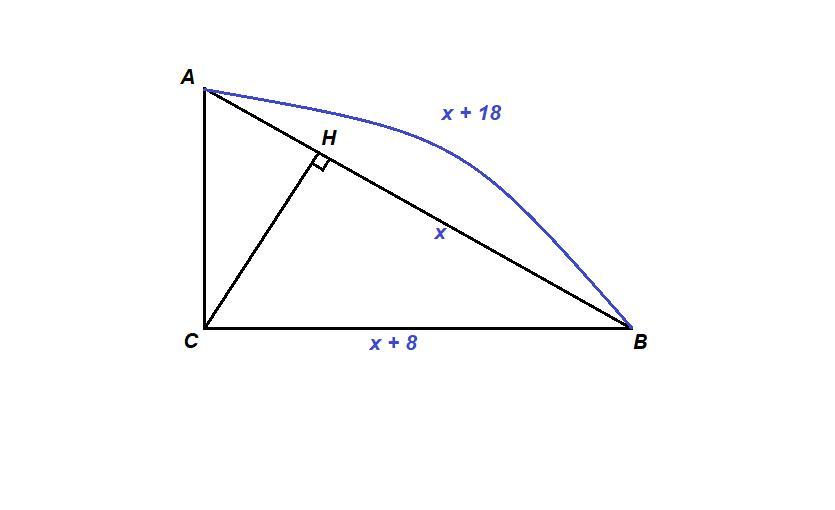
Найдите меньший катет прямоугольного треугольника и его высоту проведённую к гипотенузе, если больший катет меньше гипотенузы на 10 см и больше своей проекции на 8 см

Answer 1

Ответ:

АС = 30 см

СН = 24 см

Объяснение:

ΔАВС,  ∠С = 90°.

ВС - больший катет, СН - высота, значит НВ - проекция ВС на гипотенузу.

Обозначим:

х см - НВ,

(х + 8) см - ВС,

(х + 8 + 10) = (х + 18) см - АВ.

По свойству пропорциональных отрезков в прямоугольном треугольнике:

BC² = AB · HB

(x + 8)² = (x + 18) · x

x² + 16x + 64 = x² + 18x

2x = 64

x = 32

BC = 32 + 8 = 40 см

АВ = 32 + 18 = 50 см

По теореме Пифагора:

АС = √(АВ² - ВС²) = √(2500 - 1600) = √900 = 30 см

Из ΔСНВ по теореме Пифагора:

СН = √(ВС² - НВ²) = √(1600 - 1024) = √576 = 24 см