Предмет: Геометрия,
автор: Maryruti789
Высота CD треугольника ABC делит медиану BM в соотношении 3:1 считая от вершины B. В каком соотношении высота CD делит сторону AB?
Ответы
Автор ответа:
0
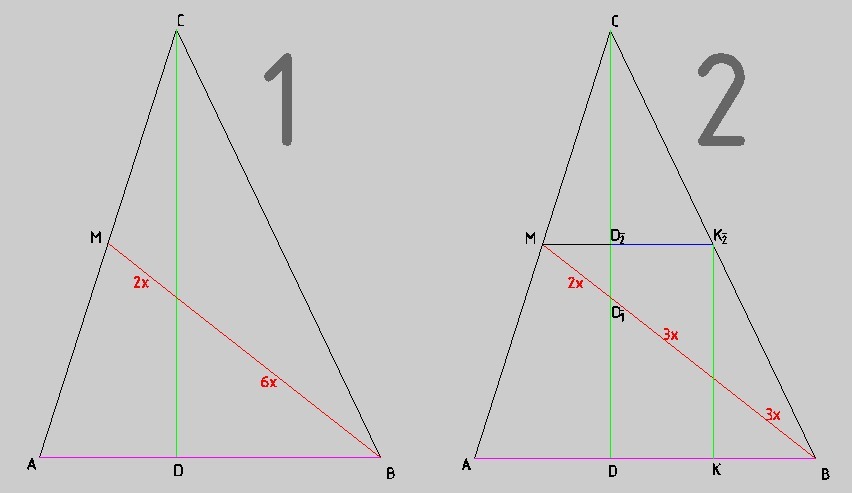
1) Исходное положение
Медиана(красная) разрезана высотой на части 2х и 6x
2:6 = 1:3, так что всё по условию.
2) Построим среднюю линию треугольника АВС, параллельную стороне АВ
3) Построим семейство прямых, параллельных высоте СД, на расстоянии х друг от друга. Медина ВМ будет разбита на две части слева от высоты СД и на 6 частей справа.
Эти же прямые разобьют среднюю линию МК₂ в соотношении - две части слева от высоты и три части справа.
4) Средняя линия даёт треугольник, подобный исходному. И деление средней линии в отношении 2 к 3 даст в итоге деление основания треугольника высотой в отношении 4 к 6. Или, сократив, тоже получим 2:3
Средняя линия - уже на части 1y и 3/2y
Ну а основание - в соотношении 2y и 3y
Ответ - 2 к 3
Медиана(красная) разрезана высотой на части 2х и 6x
2:6 = 1:3, так что всё по условию.
2) Построим среднюю линию треугольника АВС, параллельную стороне АВ
3) Построим семейство прямых, параллельных высоте СД, на расстоянии х друг от друга. Медина ВМ будет разбита на две части слева от высоты СД и на 6 частей справа.
Эти же прямые разобьют среднюю линию МК₂ в соотношении - две части слева от высоты и три части справа.
4) Средняя линия даёт треугольник, подобный исходному. И деление средней линии в отношении 2 к 3 даст в итоге деление основания треугольника высотой в отношении 4 к 6. Или, сократив, тоже получим 2:3
Средняя линия - уже на части 1y и 3/2y
Ну а основание - в соотношении 2y и 3y
Ответ - 2 к 3
Приложения:
Автор ответа:
0
А доказательство что среднюю линию делит как 2։3 ?
Автор ответа:
0
Напиши пожалуйста
Автор ответа:
0
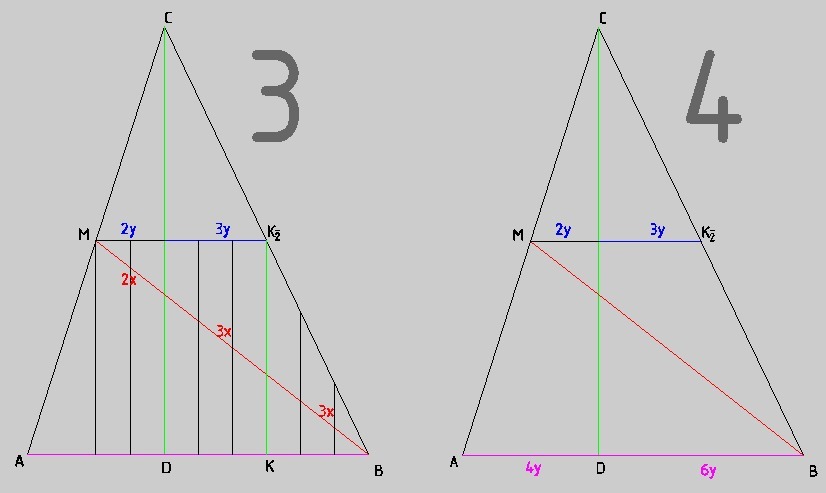
PN параллелен CD ΔCDB и ΔPNB подобны, значит BP:BC=BN:BD,
знаем что BP=PC=BC/2 => BN:BD=1:2 => BN=ND=x
так же ΔCDA ΔMKA подобны, значит AM:AC=AK:AD,
знаем что AM=MC=AC/2 => AK:AD=1:2 => AK=KD=y
ΔBOD и ΔBMK подобны=> BO:BM=BD:BK мы знаем что BO:OM=3:1
BO:BM будет как 3։4
значит BD:BK=3։4
4BD=3BK
4(BN+ND)=3(BN+ND+DK)
4(x+x)=3(x+x+y)
8x=6x+3y
x=3/2y
D делит AB на AD:DB=2y:2x=2y:3y=2:3
Ответ 2։3
знаем что BP=PC=BC/2 => BN:BD=1:2 => BN=ND=x
так же ΔCDA ΔMKA подобны, значит AM:AC=AK:AD,
знаем что AM=MC=AC/2 => AK:AD=1:2 => AK=KD=y
ΔBOD и ΔBMK подобны=> BO:BM=BD:BK мы знаем что BO:OM=3:1
BO:BM будет как 3։4
значит BD:BK=3։4
4BD=3BK
4(BN+ND)=3(BN+ND+DK)
4(x+x)=3(x+x+y)
8x=6x+3y
x=3/2y
D делит AB на AD:DB=2y:2x=2y:3y=2:3
Ответ 2։3
Приложения:
Автор ответа:
0
Треугольники подобны, а не похожи. Подобие - это математический термин
Автор ответа:
0
ага, спасибо) я термины не на русском учил) перевод не тот!
Автор ответа:
0
Тогда исправьте в доказательстве
Автор ответа:
0
не могу изменить((
Похожие вопросы
Предмет: История,
автор: rodolsplay
Предмет: Математика,
автор: katiakrupa54
Предмет: Русский язык,
автор: seregashiskin
Предмет: Физика,
автор: rrrrtttt01
Предмет: Математика,
автор: jonix5