Предмет: Алгебра,
автор: Кариночка78
Помогите, пожалуйста, найти интервалы возрастания и убывания функции. Подробно.
Приложения:
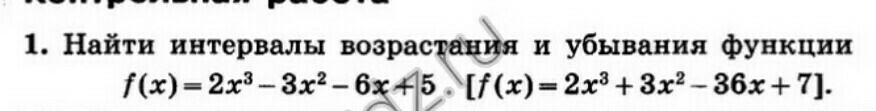
Ответы
Автор ответа:
0
функция возрастает в промежутке f'(x)>0
и убывает в промежутке f'(x)<0


и убывает в промежутке f'(x)<0
Автор ответа:
0
то что в скобке тоже нужно сделать?
Автор ответа:
0
если вас не затруднит, то помогите, пожалуйста, тоже сделать
Автор ответа:
0
без проблем, что не понятно спрашивайте
Похожие вопросы
Предмет: Українська література,
автор: zdaria37
Предмет: Химия,
автор: milchenko666
Предмет: История,
автор: CoreQ
Предмет: Математика,
автор: ююю1010
Предмет: География,
автор: mihail030304