Question

Точки M и N лежат на стороне AC треугольника ABC на расстояниях соответственно 9 и 11 от вершины A. Найдите радиус окружности, проходящей через точки M и N и касающейся луча AB, если cos угла BAC =√11/6. Пожалуйста помогите!!!!

Answer 1

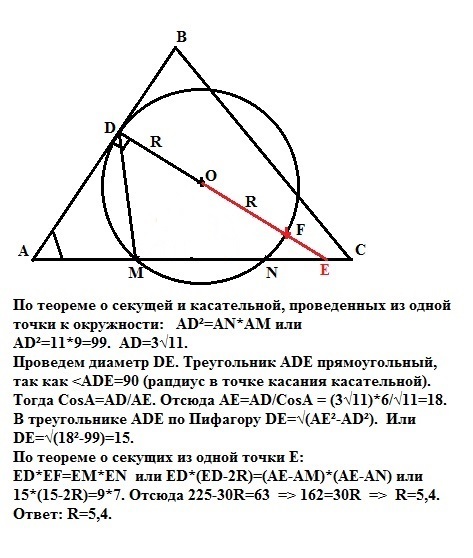
По теореме о секущей и касательной, проведенных из одной точки к окружности:   AD²=AN*AM или
AD²=11*9=99.  AD=3√11.
Проведем диаметр DE. Треугольник ADE прямоугольный, так как <ADE=90 (рапдиус в точке касания касательной).
Тогда CosA=AD/AE. Отсюда АЕ=AD/CosA = (3√11)*6/√11=18.
В треугольнике ADE по Пифагору DE=√(AE²-AD²).  Или
DE=√(18²-99)=15.  
По теореме о секущих из одной точки Е:
ED*EF=EM*EN  или ED*(ED-2R)=(AE-AM)*(AE-AN) или
15*(15-2R)=9*7. Отсюда 225-30R=63  => 162=30R  =>  R=5,4.
Ответ: R=5,4.