Предмет: Алгебра,
автор: LaLeka
Нужно подробное решение 795 номера
Приложения:
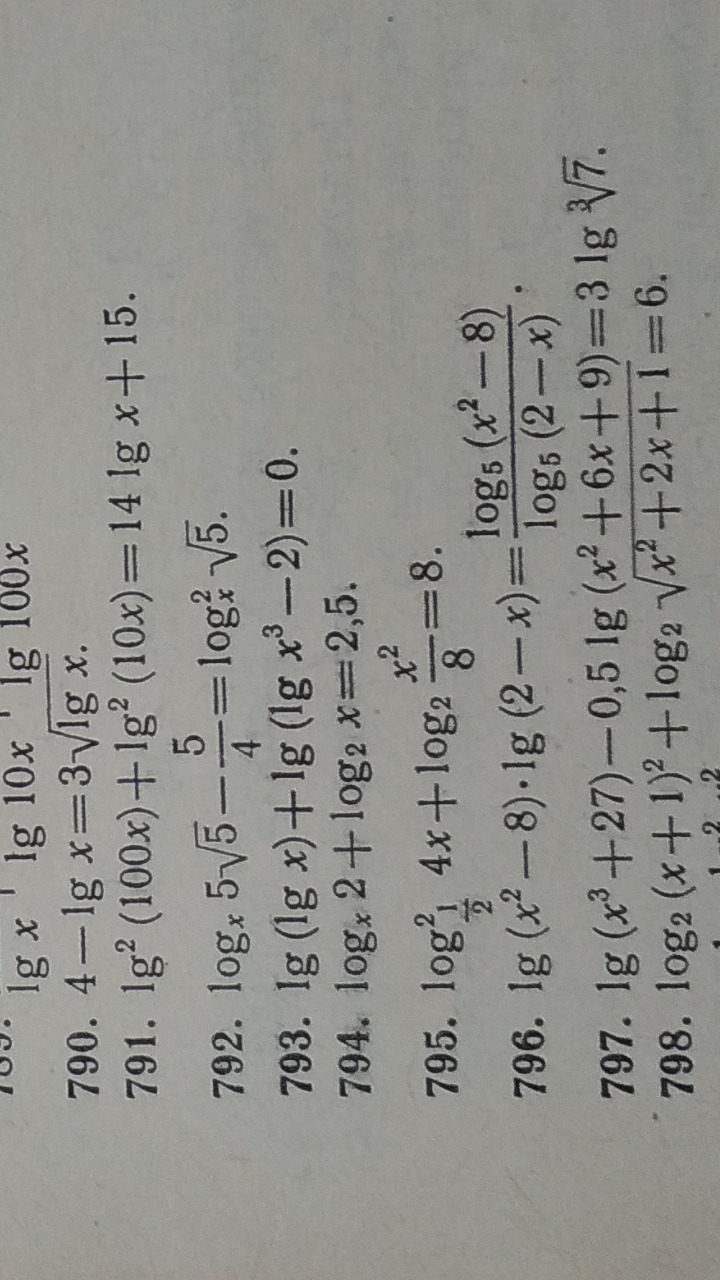
Ответы
Автор ответа:
0
log(1/2)4x=log(1/2)4+log(1/2)x=-2-log(2)x
(-2-log(2)x)²+2log(2)x-log(2)8-8=0
4+4log(2)x+log²(2)x+2log(2)x-3-8=0
log(2)x=a,x>0
a²+6a-7=0
a1+a2=-6 U a1*a2=-7
a1=-7⇒log(2)x=-7⇒x=1/128
a2=1⇒log(2)x=1⇒x=2
(-2-log(2)x)²+2log(2)x-log(2)8-8=0
4+4log(2)x+log²(2)x+2log(2)x-3-8=0
log(2)x=a,x>0
a²+6a-7=0
a1+a2=-6 U a1*a2=-7
a1=-7⇒log(2)x=-7⇒x=1/128
a2=1⇒log(2)x=1⇒x=2
Автор ответа:
0
Ответ: {2; 1/128}
Похожие вопросы
Предмет: Математика,
автор: 129978
Предмет: Математика,
автор: bazuranikita
Предмет: Биология,
автор: sakotkonikita923
Предмет: Литература,
автор: 281201