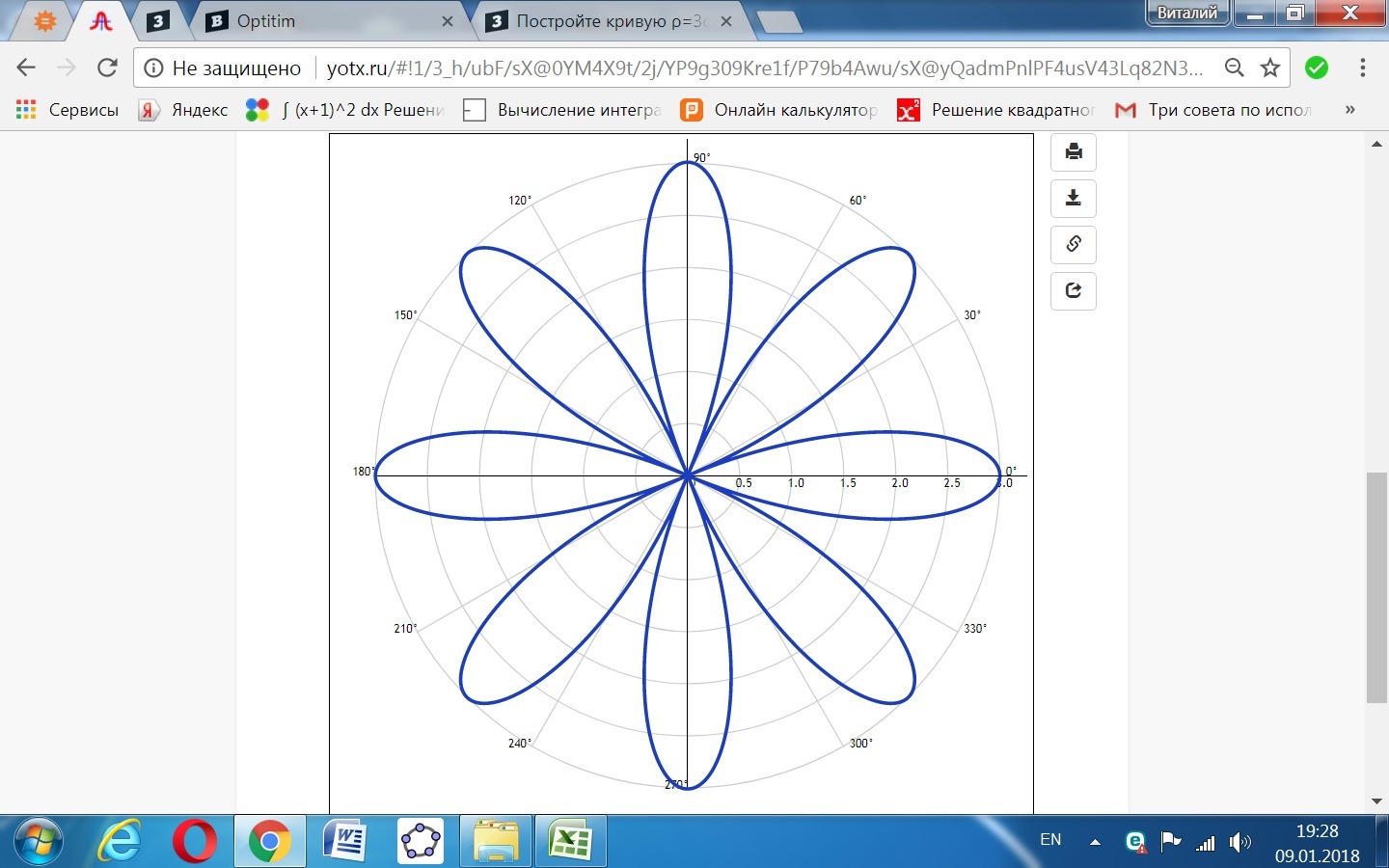
Постройте кривую ρ=3cos4φ в полярной системе координат.
Ответы
Полярная роза — известная математическая кривая, похожая на цветок с лепестками. Она может быть определена простым уравнением в полярных координатах:
{displaystyle r(varphi )=acos(kvarphi +theta _{0})}для произвольной постоянной {displaystyle theta _{0}} (включая 0). Если {displaystyle k} — целое число, то это уравнение будет определять розу с {displaystyle k} лепестками для нечётных {displaystyle k}, либо с {displaystyle 2k}лепестками для чётных {displaystyle k}. Если {displaystyle k} — рациональное, но не целое, график, заданный уравнением, образует фигуру, подобную розе, но лепестки будут перекрываться. Если {displaystyle k} — иррациональное, то роза состоит из бесконечного множества частично накладывающихся друг на друга лепестков. Розы с 2, 6, 10, 14 и т. д. лепестками этим уравнением определить невозможно. Переменная {displaystyle a}определяет длину лепестков.