Предмет: Математика,
автор: AmaliaSartre
помогите пожалуйста!!!!
Случайная величина X задана интегральной функцией распределения F(x). Требуется: 1) найти дифференциальную функцию распределения f(x); 2) найти математическое ожидание M(X) и дисперсию D(X); 3) построить графики функций F(x) и f(x).
Приложения:
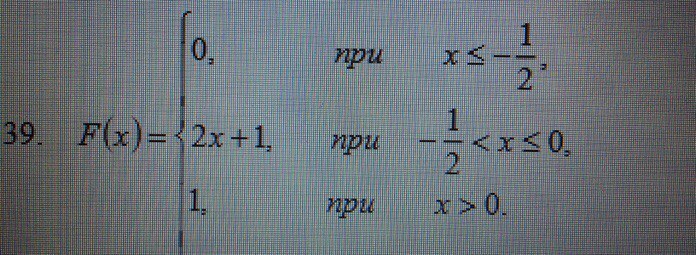
Ответы
Автор ответа:
0
По определению плотности: плотность распределения f(x) определяется, как производная от функции распределения F(x).

То есть, плотность распределения f(x) имеет следующий вид:

Хочу еще для удобства вместо обозначения случайной величины Х хочу обозначит как (можете просто наоборот).
(можете просто наоборот).
Вычислим математическое ожидание по определению

Дисперсия случайной величины по определению вычисляется следующим образом:
по определению вычисляется следующим образом:

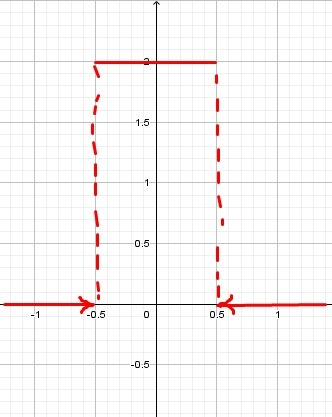
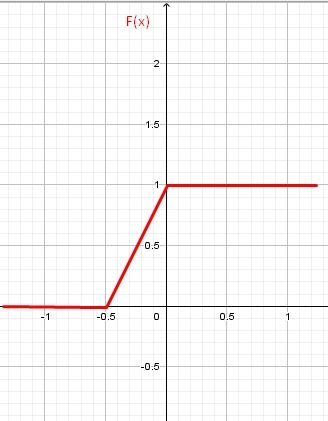
3) Графики смотрите во вложении на картинках.
То есть, плотность распределения f(x) имеет следующий вид:
Хочу еще для удобства вместо обозначения случайной величины Х хочу обозначит как
Вычислим математическое ожидание по определению
Дисперсия случайной величины
3) Графики смотрите во вложении на картинках.
Приложения:
Похожие вопросы
Предмет: История,
автор: ktoto4379
Предмет: Информатика,
автор: toliksemcuka3
Предмет: Информатика,
автор: bogdanadarnopih
Предмет: История,
автор: Аноним
Предмет: Математика,
автор: 55555homa