Question

помогите пожалуйста, срочно.

Answer 1

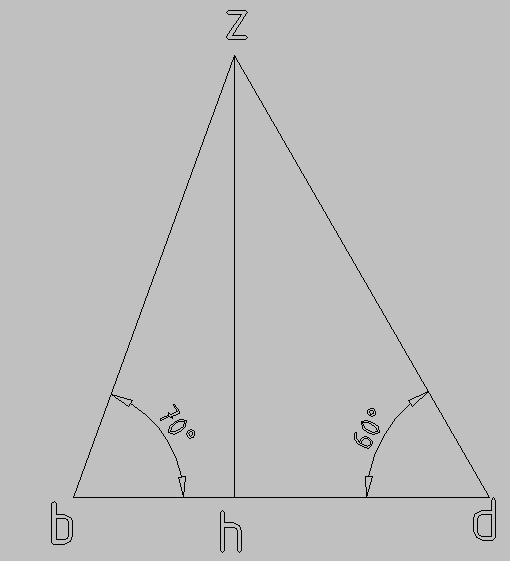
∠z = 180°-60°-70° = 50°
Это было самое простое :)
zh/bh = tg(70°)
zh/hd = tg(60°)
bh+hd = √6
Три уравнения, три неизвестных.
Высота по задаче не требуется
hd/bh = tg(70°)/tg(60°)
hd = bh*tg(70°)/tg(60°)
bh+bh*tg(70°)/tg(60°) = √6
bh = √6/(1+tg(70°)/tg(60°)) = tg(60°)√6/(tg(60°)+tg(70°))
hd = tg(70°)√6/(tg(60°)+tg(70°))
Хорошо, нижние катеты найдены, теперь гипотенузы
bh/bz = cos(70°)
bz = bh/cos(70°) = tg(60°)/cos(70°)*√6/(tg(60°)+tg(70°)) ≈ 2,6792
dz = tg(70°)/cos(60°)*√6/(tg(60°)+tg(70°)) = 3,0047
Всё :)