Предмет: Математика,
автор: Assdfhjgk
Помогите решить уравнение эту тему пропустил
Приложения:
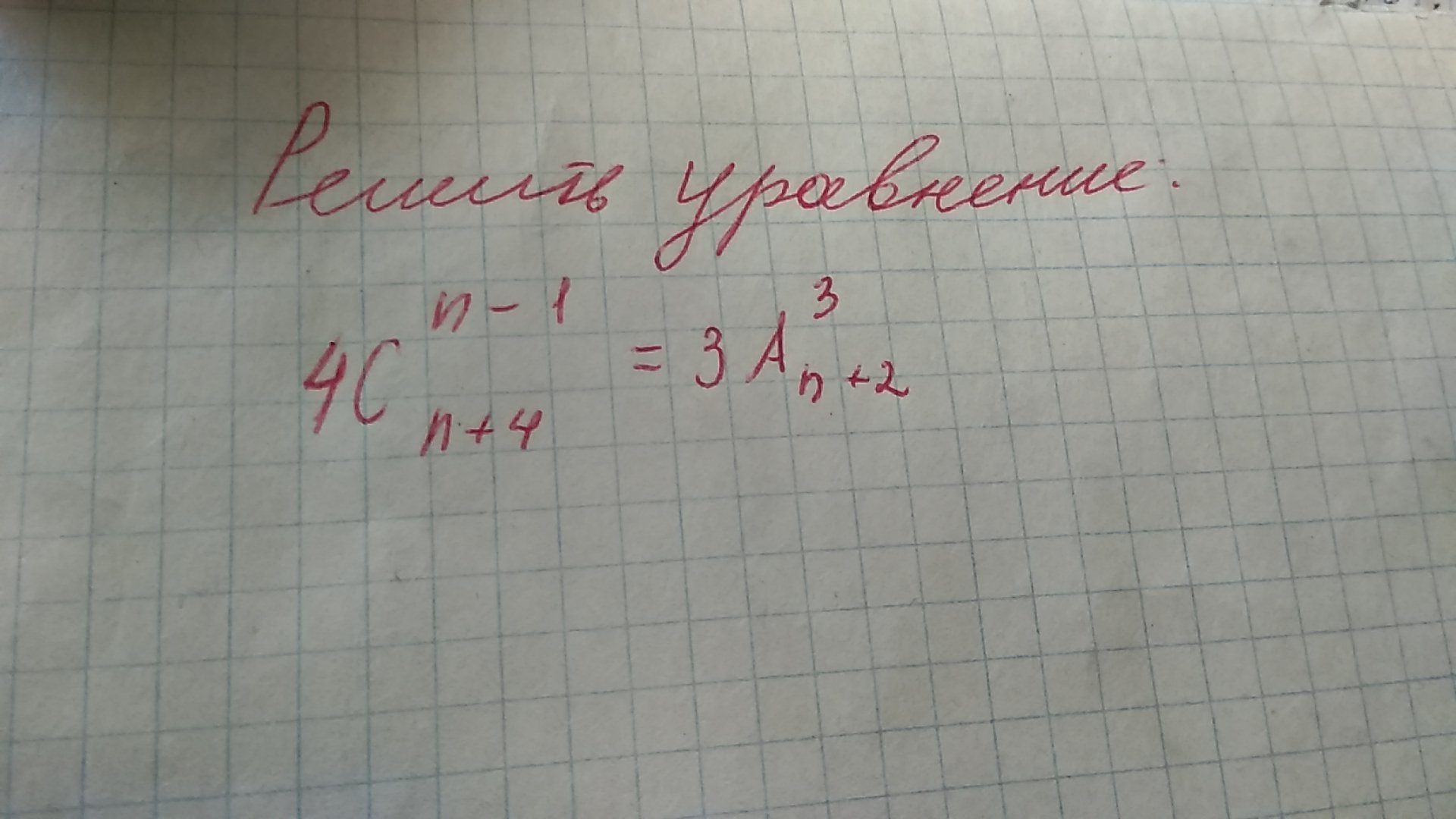
Ответы
Автор ответа:
0
Число сочетаний (без повторений) из n элементов по k:

Размещение (без повторений) из n элементов по k^

Запись n! (эн-факториал) означает произведение всех чисел от 1 до n:
n! = 1*2*3*...*n

Отрицательный корень не подходит, т.к. n > 0.
Ответ: n = 6
Размещение (без повторений) из n элементов по k^
Запись n! (эн-факториал) означает произведение всех чисел от 1 до n:
n! = 1*2*3*...*n
Отрицательный корень не подходит, т.к. n > 0.
Ответ: n = 6
Похожие вопросы
Предмет: Математика,
автор: luk08
Предмет: Математика,
автор: mariaaafytf3
Предмет: Математика,
автор: kotelenecmatvej28
Предмет: История,
автор: kamillа
Предмет: Математика,
автор: Яна200511