Предмет: Алгебра,
автор: Alepsy
Помогите вычислить определённый интеграл
Приложения:

Ответы
Автор ответа:
0
Есть 2 способа вычислить этот интеграл: сложный и простой.
Сложный способ: вычислить неопределенный интеграл, подставить в полученное выражение границы:1) x=1 и 2) х=-1, вычесть их.

Простой способ через свойство определенного интеграла: если под интегралом стоит нечетная функция и интервал интегрирования симметричен относительно x=0, то значение определенного интеграла равно 0.

Следовательно, функция - нечетная
- нечетная
Интервал [-1; 1] симметричен относительно x=0, поэтому определенный интеграл

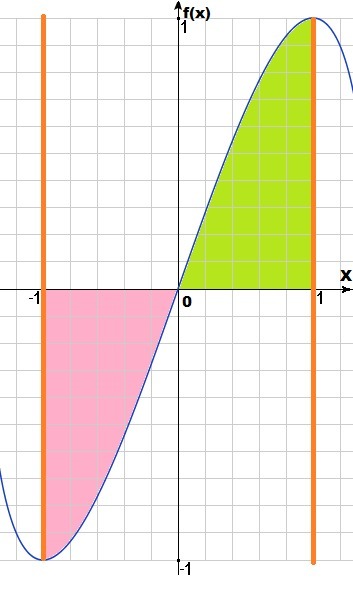
Графическое объяснение на рисунке
Определенный интеграл - это площадь криволинейной фигуры с заданными границами.
Голубая линия - это функция . Функция нечетная, поэтому симметрична относительно точки (0; 0). Если график повернуть на 180°, то он полностью совпадет.
. Функция нечетная, поэтому симметрична относительно точки (0; 0). Если график повернуть на 180°, то он полностью совпадет.
Границы интервала x=[-1;1] помечены красным цветом.
Когда считаем определенный интеграл, то, подставив верхнюю границу получаем площадь, закрашенную зеленым цветом.Подставив нижнюю границу, получаем площадь, закрашенную розовым цветом. Нужно вычесть из зеленой площади розовую. Т.к. они равны, то в результате получается 0.

Сложный способ: вычислить неопределенный интеграл, подставить в полученное выражение границы:1) x=1 и 2) х=-1, вычесть их.
Простой способ через свойство определенного интеграла: если под интегралом стоит нечетная функция и интервал интегрирования симметричен относительно x=0, то значение определенного интеграла равно 0.
Следовательно, функция
Интервал [-1; 1] симметричен относительно x=0, поэтому определенный интеграл
Графическое объяснение на рисунке
Определенный интеграл - это площадь криволинейной фигуры с заданными границами.
Голубая линия - это функция
Границы интервала x=[-1;1] помечены красным цветом.
Когда считаем определенный интеграл, то, подставив верхнюю границу получаем площадь, закрашенную зеленым цветом.Подставив нижнюю границу, получаем площадь, закрашенную розовым цветом. Нужно вычесть из зеленой площади розовую. Т.к. они равны, то в результате получается 0.
Приложения:
Автор ответа:
0
Ниче не понятно ,на листочке можете написать?
Автор ответа:
0
В какой части непонятно: в сложной или простой?
Похожие вопросы
Предмет: Литература,
автор: vikastar123321
Предмет: Химия,
автор: artyomvarlamov05
Предмет: Українська література,
автор: arikuplevatskaya
Предмет: Геометрия,
автор: PashaTehnik2401