Предмет: Математика,
автор: karinkarinaka
Пожалуйста, помогите с решением уравнения и системы
даю 45 баллов!
Приложения:
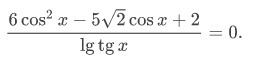

Ответы
Автор ответа:
0
Написала, ответ в закреплении
Приложения:

Автор ответа:
0
1
{16^cosx-10*4^cosx+16=0 (1)
{√y+2sinx=0 (2)
1)4^cosx=t
t²-10t+16=0
T1+t2=10 U t1*t2=16
t1=8⇒2^2cosx=3⇒cosx=1,5>1 нет решения
t2=2⇒2^2cosx=1⇒cosx=1/2⇒x=-π/3 U cosx=π/3
sinx=√(1-cos²x)=+-√(1-1/4)=+-√3/2
2)√y+2*(-√3/2)=0⇒√y=√3⇒y=3
√y+2*√3/2=0⇒√y=-√3 нет решения
Ответ (-π/3+2πk,k∈z;3)
2
ОДЗ lgtgx≠0⇒tgx≠1⇒x≠π/4+πk,k∈z
cosx=t
6t²-5√2t+2=0
D=50-48=2
t1=(5√2-√2)/12=√2/3⇒cosx=√2/3⇒x=+-arccos√2/3+2πk,k∈z
t2=(5√2+√2)/12=√2/2⇒cosx=√2/2
x=-π/4+2πk,k∈z U x=π/4+2πk,k∈z не удов ОДЗ
Ответ x={-π/4+2πk,k∈z ;+-arccos√2/3+2πk,k∈z}
{16^cosx-10*4^cosx+16=0 (1)
{√y+2sinx=0 (2)
1)4^cosx=t
t²-10t+16=0
T1+t2=10 U t1*t2=16
t1=8⇒2^2cosx=3⇒cosx=1,5>1 нет решения
t2=2⇒2^2cosx=1⇒cosx=1/2⇒x=-π/3 U cosx=π/3
sinx=√(1-cos²x)=+-√(1-1/4)=+-√3/2
2)√y+2*(-√3/2)=0⇒√y=√3⇒y=3
√y+2*√3/2=0⇒√y=-√3 нет решения
Ответ (-π/3+2πk,k∈z;3)
2
ОДЗ lgtgx≠0⇒tgx≠1⇒x≠π/4+πk,k∈z
cosx=t
6t²-5√2t+2=0
D=50-48=2
t1=(5√2-√2)/12=√2/3⇒cosx=√2/3⇒x=+-arccos√2/3+2πk,k∈z
t2=(5√2+√2)/12=√2/2⇒cosx=√2/2
x=-π/4+2πk,k∈z U x=π/4+2πk,k∈z не удов ОДЗ
Ответ x={-π/4+2πk,k∈z ;+-arccos√2/3+2πk,k∈z}
Приложения:

Похожие вопросы
Предмет: Физика,
автор: ychenick0
Предмет: История,
автор: Аноним
Предмет: Кыргыз тили,
автор: Saul33
Предмет: История,
автор: Кличко1337
Предмет: Математика,
автор: захарнезнайка