Предмет: Алгебра,
автор: Natahakl
Помогите пожалуйста решить 13,16,19 неравенства иррациональные
Приложения:

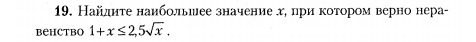
Ответы
Автор ответа:
0
13
√(x²-16)/√(x-3)+(x-3)/√(x-3)-5/√(x-3)>0
√(x²-16)/√(x-3)+(x-8)/√(x-3)>0
(√(x²-16)+x-8)/√(x-3)>0
ОДЗ
{(x-4)(x+4)≥0⇒x≤-4 U x≥4
{x-3>0⇒x>3
x∈[4;∞)
Так как √(x-3)>0 на всей ОДЗ⇒√(x²-16)+x-8>0
√(x²-16)>8-x
возведем в квадрат
x²-16>64-16x+x²
16x>80
x>5
Ответ x∈(5;∞)
16
![1,5 sqrt[6]{x+1} -1 geq 0,5 sqrt[3]{x+1} 1,5 sqrt[6]{x+1} -1 geq 0,5 sqrt[3]{x+1}](https://tex.z-dn.net/?f=1%2C5+sqrt%5B6%5D%7Bx%2B1%7D+-1+geq+0%2C5+sqrt%5B3%5D%7Bx%2B1%7D+)
x+1≥0⇒x≥-1
![sqrt[6]{x+1} =t sqrt[6]{x+1} =t](https://tex.z-dn.net/?f=+sqrt%5B6%5D%7Bx%2B1%7D+%3Dt)
0,5t²-1,5t+1≤0
t²-3t+2≤0
t1+t2=3 U t1*t2=2⇒t1=1 U t2=2
1≤t≤2
![1 leq sqrt[6]{x+1} leq 2 1 leq sqrt[6]{x+1} leq 2](https://tex.z-dn.net/?f=1+leq++sqrt%5B6%5D%7Bx%2B1%7D++leq+2)
1≤x+1≤64
0≤x≤63
Ответ x∈[0;63]
19
1+x≤2,5√x
x≥0
√x=t
t²-2,5t+1≤0
t1+t2=2,5 U t1*t2=1⇒t1=0,5 U t2=2
0,5≤t≤2
0,5≤√x≤2
0,25≤x≤4
Ответ x∈[0,25;4]
√(x²-16)/√(x-3)+(x-3)/√(x-3)-5/√(x-3)>0
√(x²-16)/√(x-3)+(x-8)/√(x-3)>0
(√(x²-16)+x-8)/√(x-3)>0
ОДЗ
{(x-4)(x+4)≥0⇒x≤-4 U x≥4
{x-3>0⇒x>3
x∈[4;∞)
Так как √(x-3)>0 на всей ОДЗ⇒√(x²-16)+x-8>0
√(x²-16)>8-x
возведем в квадрат
x²-16>64-16x+x²
16x>80
x>5
Ответ x∈(5;∞)
16
x+1≥0⇒x≥-1
0,5t²-1,5t+1≤0
t²-3t+2≤0
t1+t2=3 U t1*t2=2⇒t1=1 U t2=2
1≤t≤2
1≤x+1≤64
0≤x≤63
Ответ x∈[0;63]
19
1+x≤2,5√x
x≥0
√x=t
t²-2,5t+1≤0
t1+t2=2,5 U t1*t2=1⇒t1=0,5 U t2=2
0,5≤t≤2
0,5≤√x≤2
0,25≤x≤4
Ответ x∈[0,25;4]
Похожие вопросы
Предмет: Русский язык,
автор: knijmatova
Предмет: Информатика,
автор: nicolborisov2
Предмет: Геометрия,
автор: vorobushekzn
Предмет: Математика,
автор: полина14122007