Предмет: Алгебра,
автор: archer141201
Пожалуйста помогите с тригонометрией. Буду очень благодарен.
Приложения:
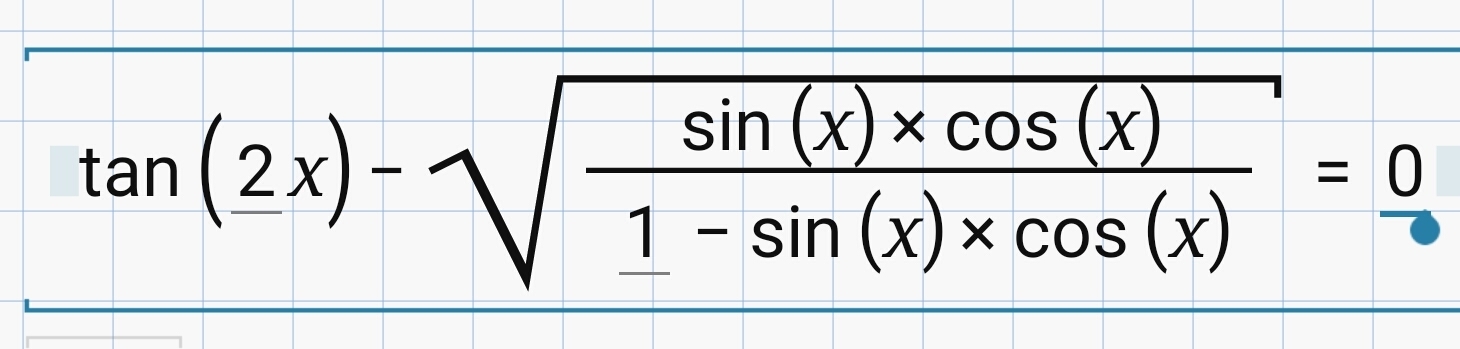
Ответы
Автор ответа:
0
task/27210604
--------------------
tg(2x) - √[ sin(x)*cos(x) / (1 - sin(x)*cos(x) ) ] =0 ;
tg(2x) = √[ 2sin(x)*cos(x) / (2 - 2sin(x)*cos(x) ) ] ;
tg(2x) = √[ sin(2x) / (2 - sin(2x) ) ] ; т.к. 2 - sin(2x) > 0 ,то
ОДЗ: { sin(2x) ≥ 0 , cos2x ≠ 0.
-----------
Уравнение имеет решений,если tq2x ≥ 0 ,что с учетом ОДЗ,означает :
{ sin(2x) ≥ 0 , cos(2x) > 0 .
-----------
tg²(2x) = sin(2x) / (2 - sin(2x) ) ;
sin²(2x)*(2 - sin(2x) ) =sin(2x) *cos²(2x) ;
sin(2x)*( cos²(2x) - 2sin(2x)+sin²(2x) ) = 0 ;
sin(2x)*( 1 - 2sin(2x) ) = 0 ;
---
а)
sin(2x)= 0 ⇒ 2x =2πk , k∈ Z ⇔
x =πk , k∈ Z .
---
б)
1 - 2sin(2x) = 0 ;
sin(2x) =1/2 ;
2x =π/6 + 2πk , k∈ Z ⇔
x=π/12 + πk , k∈ Z .
ответ : πk , π/12 + πk , k∈ Z .
--------------------
tg(2x) - √[ sin(x)*cos(x) / (1 - sin(x)*cos(x) ) ] =0 ;
tg(2x) = √[ 2sin(x)*cos(x) / (2 - 2sin(x)*cos(x) ) ] ;
tg(2x) = √[ sin(2x) / (2 - sin(2x) ) ] ; т.к. 2 - sin(2x) > 0 ,то
ОДЗ: { sin(2x) ≥ 0 , cos2x ≠ 0.
-----------
Уравнение имеет решений,если tq2x ≥ 0 ,что с учетом ОДЗ,означает :
{ sin(2x) ≥ 0 , cos(2x) > 0 .
-----------
tg²(2x) = sin(2x) / (2 - sin(2x) ) ;
sin²(2x)*(2 - sin(2x) ) =sin(2x) *cos²(2x) ;
sin(2x)*( cos²(2x) - 2sin(2x)+sin²(2x) ) = 0 ;
sin(2x)*( 1 - 2sin(2x) ) = 0 ;
---
а)
sin(2x)= 0 ⇒ 2x =2πk , k∈ Z ⇔
x =πk , k∈ Z .
---
б)
1 - 2sin(2x) = 0 ;
sin(2x) =1/2 ;
2x =π/6 + 2πk , k∈ Z ⇔
x=π/12 + πk , k∈ Z .
ответ : πk , π/12 + πk , k∈ Z .
Похожие вопросы
Предмет: Математика,
автор: A14062011
Предмет: Математика,
автор: Аноним
Предмет: Алгебра,
автор: Аноним
Предмет: Алгебра,
автор: kirillpetrov02
Предмет: Математика,
автор: 2006mari