Предмет: Математика,
автор: zhenyazhukovec
пользуясь критерием Михайлова иследоватт устойчивость нцлевого решения y'''''+4y''''+9y'''+16y''+10y'+13y=0
Ответы
Автор ответа:
0
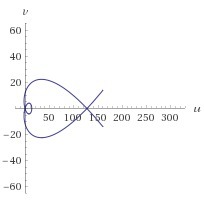
Составляя характеристический многочлен

найдем следующее значение функции:


Если то
то 
Если , то
, то 
Если , то
, то 
Если , то
, то 
Если , то
, то 
И очевидно, что
Угол поворота вектора равен и т.к. n=5, то и m=0. То есть, все корни характеристического уравнения лежат в правой полуплоскости. Решение - тривиально асимптотически устойчиво
и т.к. n=5, то и m=0. То есть, все корни характеристического уравнения лежат в правой полуплоскости. Решение - тривиально асимптотически устойчиво
найдем следующее значение функции:
Если
Если
Если
Если
Если
И очевидно, что
Угол поворота вектора равен
Приложения:
Похожие вопросы
Предмет: Українська література,
автор: Mimika2009love
Предмет: Русский язык,
автор: dilbarsaidhodjaeva
Предмет: Алгебра,
автор: valeriyturkovskay5
Предмет: Математика,
автор: sulta0404
Предмет: Математика,
автор: іііііі1