Предмет: Геометрия,
автор: dldkdkkec
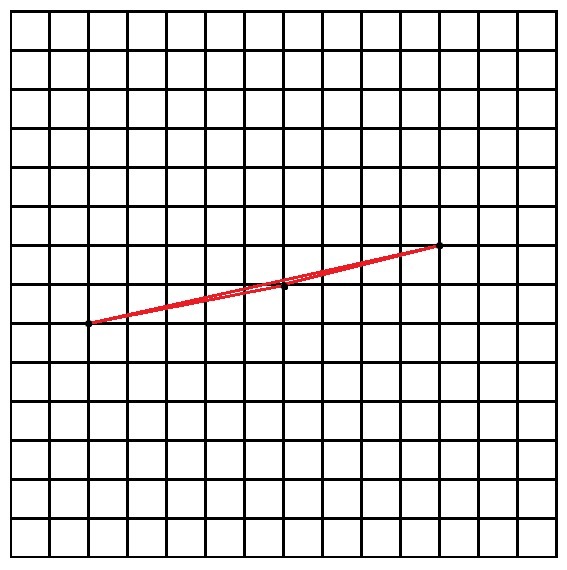
Нарисуйте треугольник с вершинами в узлах квадратной сетки со стороной 1, у которого все стороны длиннее 4, а площадь меньше 1.
Ответы
Автор ответа:
0
В данном треугольнике каждая сторона больше 4, что можно доказать теоремой Пифагора (если рассматривать прямоугольные треугольники, где сторона начерченного является гипотенузой. Один из катетов везде больше или равен 4, другой - больше или равен 1, значит, гипотенуза больше большего, скажем так).
Разберёмся с площадью.
Площадь треугольника находится по формуле , отсюда:
, отсюда: 
Пусть h - высота, проведённая к большей стороне, a - большая сторона. По теореме Пифагора она равна . Тогда
. Тогда 
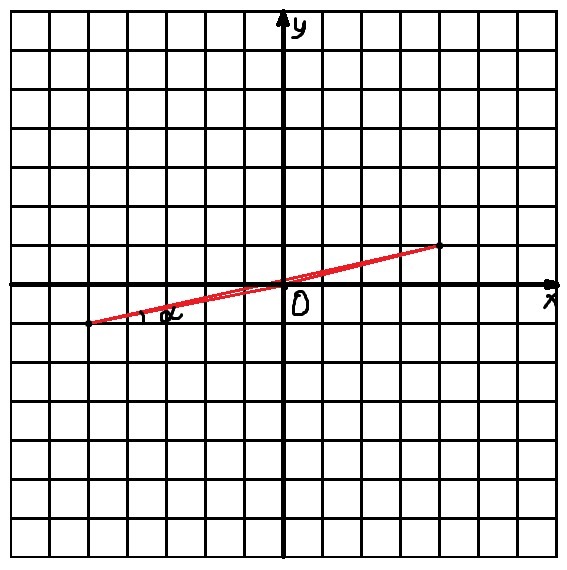
Рассмотрим треугольник в системе координат с точкой, лежащей против большей стороны, в начале координат. Найдём уравнение прямой, на которой лежит большая сторона (y=kx+b). ,
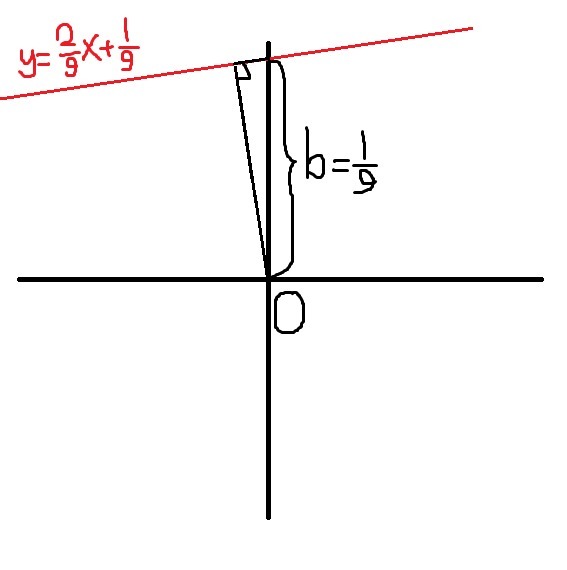
,  . Теперь рассмотрим прямоугольный треугольник из высоты и стороны на Oy, равной b. Действительно, если точка лежит на оси Oy, то её координата по x = 0, а значит, её координата y = k * 0 + b = b. В данном случае сторона на Oy будет гипотенузой, а высота - катетом. Следовательно, она меньше гипотенузы. Т. е.
. Теперь рассмотрим прямоугольный треугольник из высоты и стороны на Oy, равной b. Действительно, если точка лежит на оси Oy, то её координата по x = 0, а значит, её координата y = k * 0 + b = b. В данном случае сторона на Oy будет гипотенузой, а высота - катетом. Следовательно, она меньше гипотенузы. Т. е.  (доказательство того, что
(доказательство того, что  , могу провести в комментариях, если потребуется), значит,
, могу провести в комментариях, если потребуется), значит,  . Начерченный треугольник удовлетворяет всем условиям.
. Начерченный треугольник удовлетворяет всем условиям.
Разберёмся с площадью.
Площадь треугольника находится по формуле
Пусть h - высота, проведённая к большей стороне, a - большая сторона. По теореме Пифагора она равна
Рассмотрим треугольник в системе координат с точкой, лежащей против большей стороны, в начале координат. Найдём уравнение прямой, на которой лежит большая сторона (y=kx+b).
Приложения:
Похожие вопросы
Предмет: Физика,
автор: holew
Предмет: Оʻzbek tili,
автор: Pubg12chiter
Предмет: Физика,
автор: saidasr32
Предмет: Математика,
автор: Аноним