Question

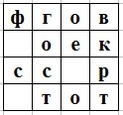
Мистер Фокс прочитал про шифр “решетка” и решил тоже что-нибудь зашифровать. Он взял квадрат 4 на 4 и сделал из него трафарет для шифра таким образом: вырезал четыре клеточки так, что если полученную решетку положить на лист бумаги 4 на 4 всеми четырьмя возможными способами и при каждом положении закрашивать те клетки, которые оказываются в дырках трафарета, то весь квадрат окажется закрашенным. Итак, приготовив трафарет, он выбрал фразу и стал ее шифровать. Мистер Фокс кладет трафарет на лист 4 на 4, записывает в дырки трафарета начало своей фразы (по строкам сверху вниз, в каждой строке слева направо), потом кладет трафарет в другое положение и пишет следующие буквы фразы и так далее. Пробелы при этом не записываются. После того, как он в последний раз положил трафарет, а затем его убрал, остался такой рисунок: (Ниже смотрите. Вложение 1)Расшифруйте фразу. В ответ запишите ее маленькими русскими буквами без пробелов между словами.

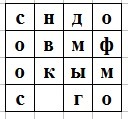
Комментарий. Чтобы условие было понятнее, приведем пример трафарета и зашифрованной фразы. Примером трафарета может быть квадрат 4 на 4 с вырезанным угловым квадратом 2 на 2 (но, конечно, мистер Фокс придумал трафарет поинтереснее). Если бы вы захотели с помощью такого простого трафарета зашифровать фразу сновымгодомфокс, то после шифровки мог бы остаться такой квадрат:

Answer 1

Подробнее о решётках я в своё время читал в книге:
 Я. И. Перельман "Живая математика". главу уже не помню. Там кстати рекомендовалось оставшиеся пустые поля заполнять произвольными буквами, чтоб дешифровальщикам жизнь мёдом не казалась. Ну раз уж Фокс так оплошал, у нас неплохие шансы.
 При шифровании решёткой 4х4 в ней можно вырезать только 4 окошка. Причём не абы как, а в определённом порядке. ( Так, чтобы они при перестановке решётки не попадали на уже записанные буквы.)
 Порядок положений решётки определим по приведённому вусловии примеру.
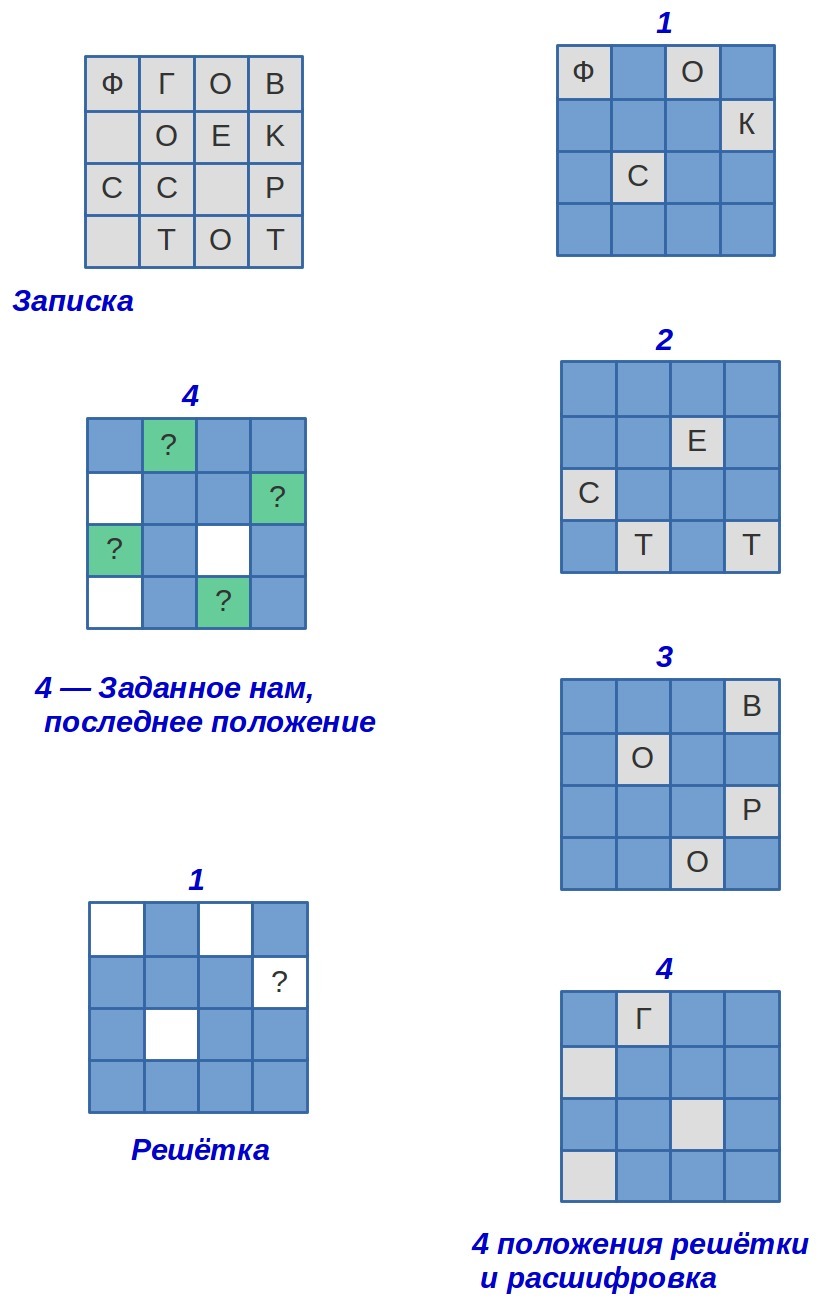
 У нас сразу есть три окошка из 4х. (Смотрите картинку) А четвёртое можно будет выбирать из 4ч вариантов на картинке (зелёные квадраты с вопросиками).
Читаем 1-е слово в 1м положении решётки. Напрашивается  фокс. Ну предположим что решётка будет иметь вид как на 3м нижнем рисунке в 1м столбце. Расшифровываем и ...

ОТВЕТ: фоксесттворог  ("Фокс ест творог", я так полагаю.)

6f552637c55ef0a7a3f23ec85ebcc295.pdf