Предмет: Алгебра,
автор: bertain
Решить примеры во вложении:
Приложения:
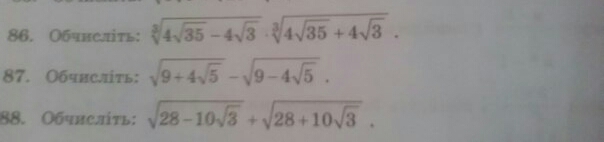
Ответы
Автор ответа:
0
',".',".',".'.',"."",',','.",''
Приложения:

Автор ответа:
0
87) выделим полный квадрат:
аналогично будет и cо 2 корнем:
теперь вычисляем значение выражения:
88) здесь тоже будем выделять полный квадрат:
аналогично и с другим корнем:
вычислим значение выражения:
Приложения:

Похожие вопросы
Предмет: Литература,
автор: koshkakartoshkaasd
Предмет: Математика,
автор: mila2134567
Предмет: Математика,
автор: parsley1
Предмет: Литература,
автор: masanovaliza