Question

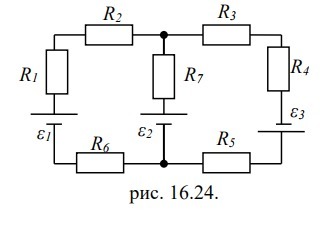
В схеме, изображенной на рис. 16.24, ε1=10,0В, ε2=20,0 В,
ε3=30,0В, R1=1,0 Ом, R2=2,0 Ом, R3= 3,0 Ом, R4=4,0 Ом, R5=5,0 Ом,
R6=6,0 Ом и R7=7,0 Ом. Внутреннее сопротивление источников
пренебрежимо мало. Определите: 1) величины токов во всех участках цепи; 2) работу, совершенную вторым источником за промежуток
времени Δt=0,1 с.
Ответ: I1= 0,6 А, I2= 2,2 А, I3= 2,8 А, А2=4,4 Дж

Answer 1

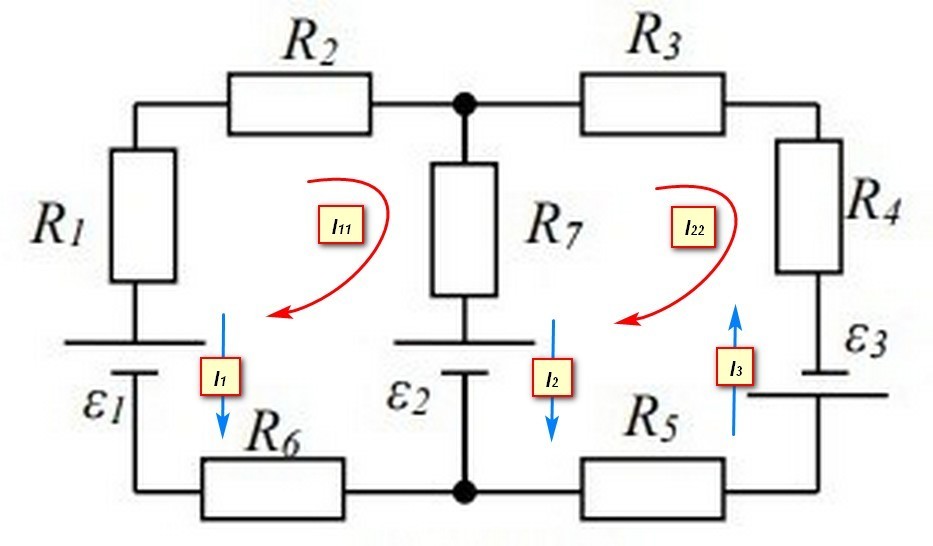
Воспользуемся методом контурных токов. Выделим два независимых контура. Первый образован элементами R₁, R₂, R₇, E₂, R₆, E₁, второй - элементами R₃, R₄, E₃, R₅, E₂, R₇.
Направим в каждом контуре контурные токи I₁₁ и I₂₂ по часовой стрелке. Токи, протекающие через источники, направим от плюса к минусу.
Для каждого контура запишем уравнение по второму закону Кирхгофа
$displaystyle left { {{I_{11}(R_1+R_2+R_7+R_6)-I_{22}cdot R_7=E_2-E_1} atop {-I_{11}cdot R_7+I_{22}(R_3+R_4+R_5+R_7)=-E_3-E_2}} right.$
Подставляем числовые данные
$displaystyle left { {{I_{11}(1+2+7+6)-I_{22}cdot 7=20-10} atop {-I_{11}cdot 7+I_{22}(3+4+5+7)=-30-20}} right. \ \ \ left { {{16cdot I_{11}-7cdot I_{22}=10} atop {-7cdot I_{11}+19cdot I_{22}=-50}} right.$
Решаем полученную систему уравнений по правилу Крамера.
$displaystyle Delta=255; quad Delta_{11}=-160; quad Delta_{22}=-730 \ \ I_{11}= -frac{160}{255}= -frac{32}{51}approx -0.63 \ \ I_{22}=- frac{730}{255}=- frac{146}{51}approx -2.86 \ \ I_1=0.63, quad I_3=2.86, quad I_2=I_3-I_1=2.23 \ \ A_2=E_2I_2cdot0.1=20cdot2.23cdot0.1approx4.46$

Answer 2

Спасибо :)

Answer 3

Пожалуйста