Question

В прямоугольной трапеции острый угол равен 60° . Большая боковая сторона и большее основание равны по 12 см. Найдите периметр трапеции. кто четко и нормально напишет дам 100 баллов!!!

Answer 1

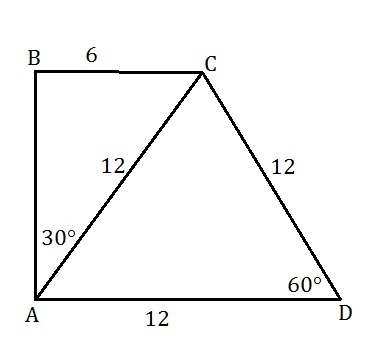
рисунок в приложении.
Проведем диагональ AC, получим треугольник ACD у которого AD=CD=12 и угол D=60°. Так как AD=CD => треуг. равноб. => угол ACD=углу DAC. по теореме о сумме углов треугольника:
угол ACD+ угол DAC+угол D=180°
2 угла ACD=120
угол ACD=уголDAC=120/2=60°, все углы равны => треугольник равносторонний =>AC=12.
рассмотрим треугольник ABC - он прямоугольный(угол B=90°).
так как угол A=90°(прямоуг. трапеция) => угол BAC=90-угол DAC=90-60=30°. В треуг. ABC AC - гипотенуза. А катет, лежащий против угла в 30° равен половине гипотенузы => BC=(1/2)*AC=12/2=6
найдем AB по теореме Пифагора:
$AC^2=AB^2+BC^2 \AB=sqrt{12^2-6^2}=sqrt{108}=6sqrt{3}$
И теперь находим периметр:
$P=AB+BC+CD+AD=6sqrt{3}+6+12+12=30+6sqrt{3}$
Ответ: $30+6sqrt{3}$