Предмет: Математика,
автор: Garri01
Найти производные. Помогите пожалуйста
Приложения:
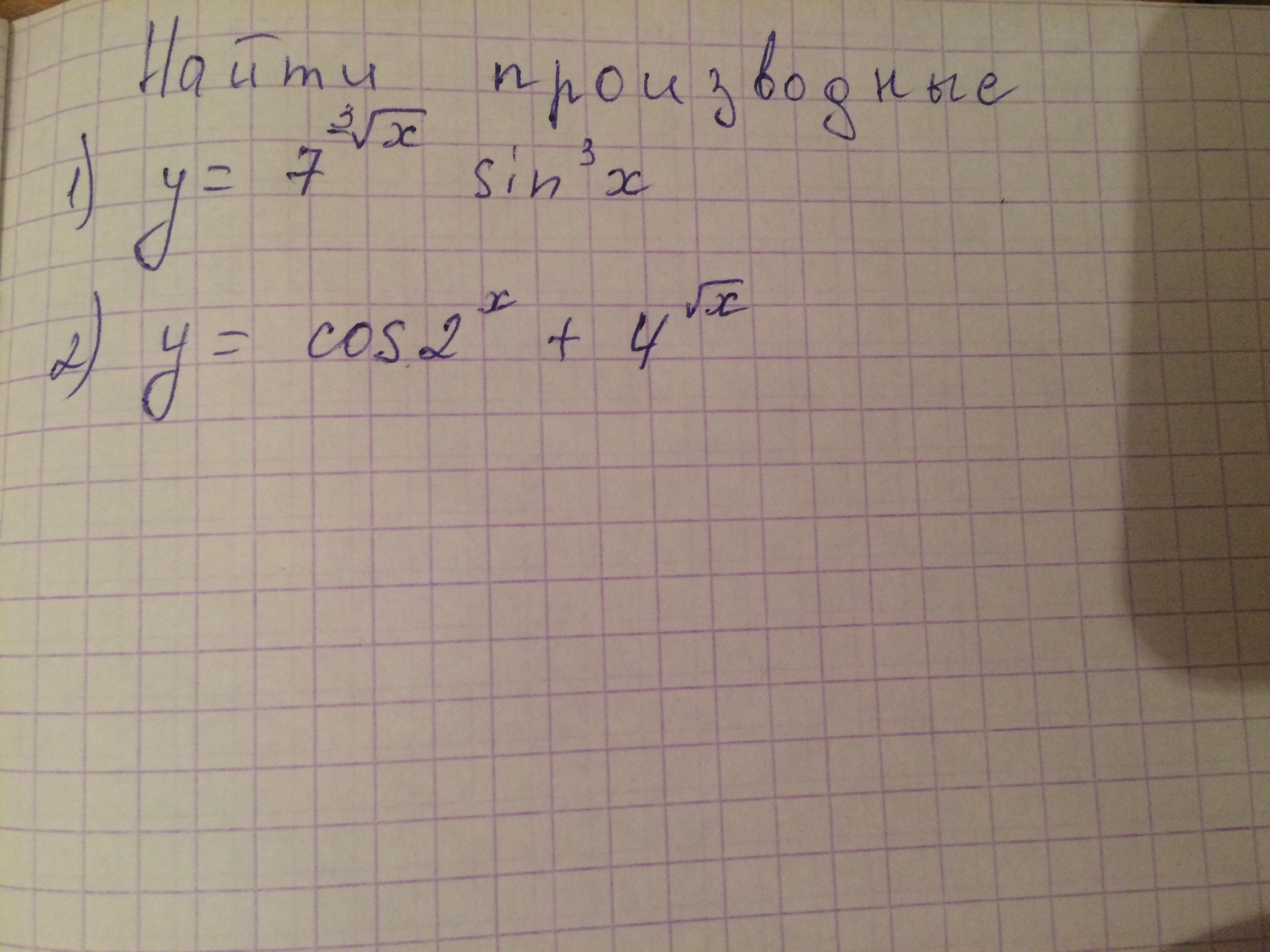
Ответы
Автор ответа:
0
1)
![(7^{sqrt[3]{x}} * sin x)'=(7^{sqrt[3]{x}})' * sin x + 7^{sqrt[3]{x}} * (sin x)'=\
= (sqrt[3]{x})' * 7^{sqrt[3]{x}} * ln 7 * sin x + 7^{sqrt[3]{x}} * cos x=\=
{7^{sqrt[3]{x}} * ln 7 * sin xover 3sqrt[3]{x^2}} + 7^{sqrt[3]{x}} * cos x (7^{sqrt[3]{x}} * sin x)'=(7^{sqrt[3]{x}})' * sin x + 7^{sqrt[3]{x}} * (sin x)'=\
= (sqrt[3]{x})' * 7^{sqrt[3]{x}} * ln 7 * sin x + 7^{sqrt[3]{x}} * cos x=\=
{7^{sqrt[3]{x}} * ln 7 * sin xover 3sqrt[3]{x^2}} + 7^{sqrt[3]{x}} * cos x](https://tex.z-dn.net/?f=%287%5E%7Bsqrt%5B3%5D%7Bx%7D%7D+%2A+sin+x%29%27%3D%287%5E%7Bsqrt%5B3%5D%7Bx%7D%7D%29%27+%2A+sin+x+%2B+7%5E%7Bsqrt%5B3%5D%7Bx%7D%7D+%2A+%28sin+x%29%27%3D%5C%0A%3D+%28sqrt%5B3%5D%7Bx%7D%29%27+%2A+7%5E%7Bsqrt%5B3%5D%7Bx%7D%7D+%2A+ln+7+%2A+sin+x+%2B+7%5E%7Bsqrt%5B3%5D%7Bx%7D%7D+%2A+cos+x%3D%5C%3D%0A%7B7%5E%7Bsqrt%5B3%5D%7Bx%7D%7D+%2A+ln+7+%2A+sin+xover+3sqrt%5B3%5D%7Bx%5E2%7D%7D+%2B+7%5E%7Bsqrt%5B3%5D%7Bx%7D%7D+%2A+cos+x)
2)

2)
Похожие вопросы
Предмет: Геометрия,
автор: nikolajkatciev9
Предмет: Другие предметы,
автор: Taelknow
Предмет: Математика,
автор: poljgccfdr
Предмет: Математика,
автор: кирилл416
Предмет: Математика,
автор: Аноним