Предмет: Алгебра,
автор: Шаен
найти определенный интеграл
Приложения:
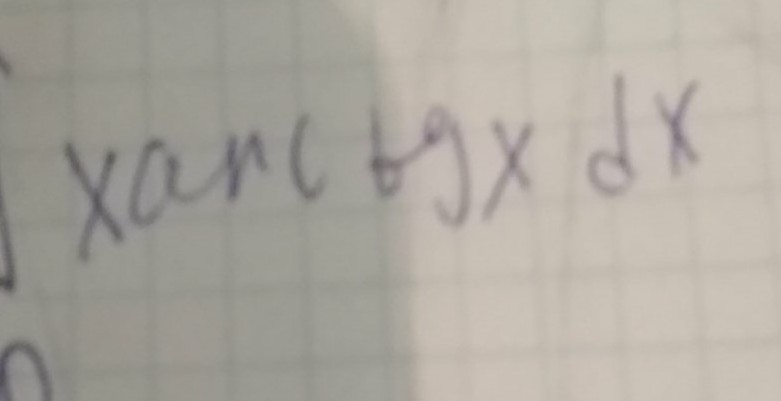
Ответы
Автор ответа:
0
интегрируем по частям неопределенный интеграл:

u=arctgx =>
dv=xdx =>


теперь решаем определенный интеграл:

u=arctgx =>
dv=xdx =>
теперь решаем определенный интеграл:
Автор ответа:
0
...............................................................
Приложения:

Похожие вопросы
Предмет: МХК,
автор: anastasyaandrushchen
Предмет: Английский язык,
автор: ayazhankyn
Предмет: Физика,
автор: vikysya808
Предмет: Алгебра,
автор: njkita2015
Предмет: География,
автор: Катюша1013139