Question

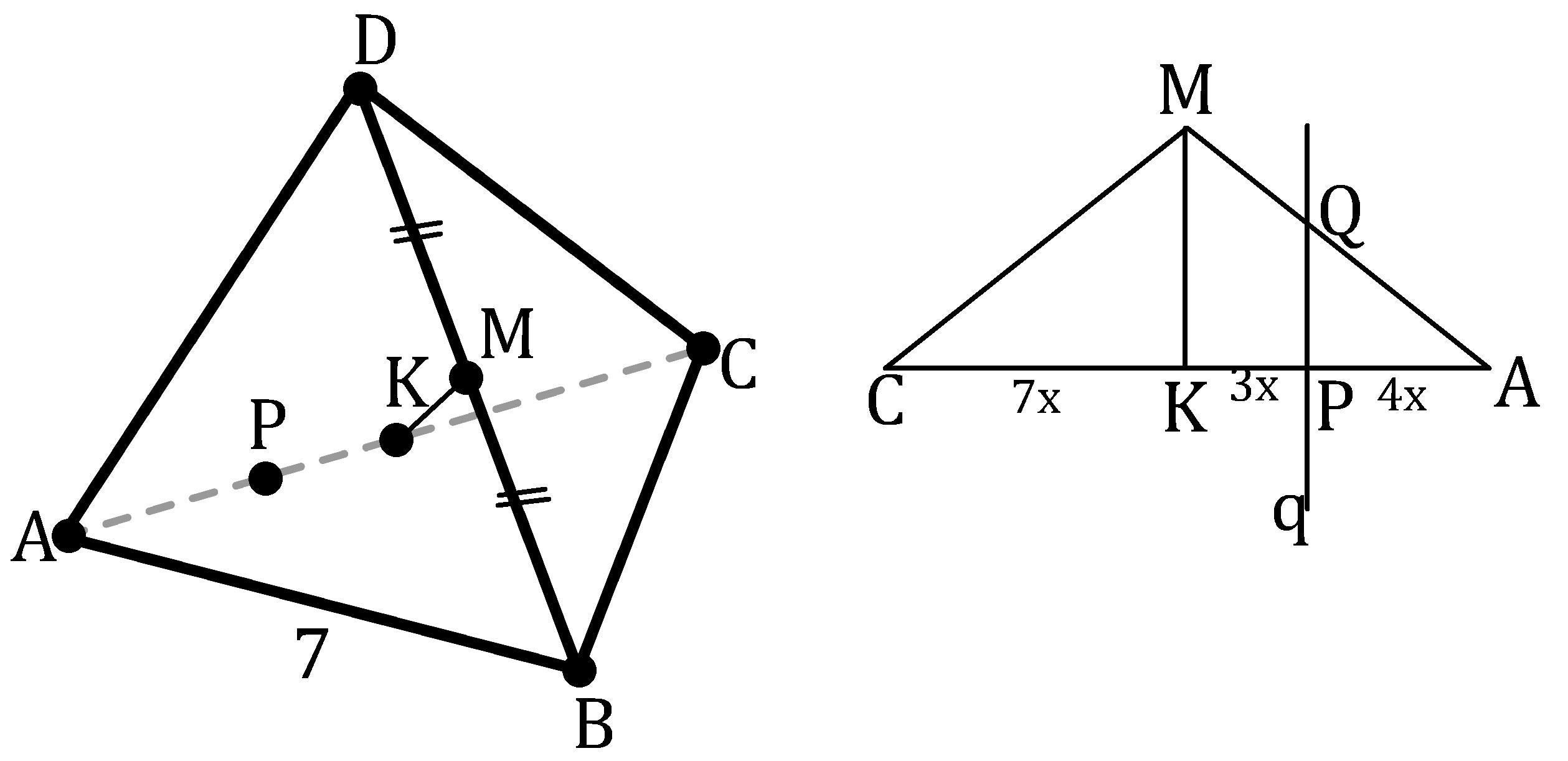
ABCD - правильный тетраэдр с длиной ребра AB=7. Точки M и K - середины ребер BD и AC соответственно. Точка P делит ребро AC в отношении 5:2.найдите длину отрезка прямой,проходящей через точку P параллельно прямой KM, заключенного внутри тетраэдра

Answer 1

ABCD - правильный тетраэдр, поэтому все его грани это правильные треугольники.

K - середина AC; KD = KB как медианы в равных и правильных треугольниках. KM⊥DB т.к. в равнобедренном треугольнике (ΔDKB), медиана опущенная на основание это и высота.

$DK=frac{sqrt{3}}{2}cdot AD=frac{sqrt{3}}{2}cdot 7$ как высота в правильном треугольника.

$DM=DB:2=frac{7}{2}$

Найдём неизвестный катет в прямоугольном ΔDMK:

$KMsqrt{DK^2-DM^2}=frac{7}{2}cdot sqrt{3-1}=frac{7sqrt{2}}{2}$

Рассмотрим ΔAMC: K, P∈AC; P∈q║KM; q∩AM=Q.

ΔMKA~ΔQPA по трём углам т.к. PQ║KM.

AK=KC - по условию. Пусть AK = 7x ⇒ AC = 14x.

CP:PA=10x:4x=5:2 ⇒ AP:AK=4x:7x=4:7, коэффициент подобия.

Найдём PQ через подобие треугольников.

$PQ=MKcdot frac{4}{7}=frac{7sqrt{2}cdot 4}{2cdot 7}=2sqrt{2}$

Ответ: 2√2.

Про точку P: по условию P может так же лежать между С и K, но ответ будет тем же т.к. точка P не влияет на длину KM, и коэффициент подобия не изменится, только он будет для других треугольников.