Предмет: Алгебра,
автор: дашадашадаша3232
Решите уравнение:
2x+6/x^2+x - x-3/x^2+3x+2=0
Алгебра 10 класс
Приложения:
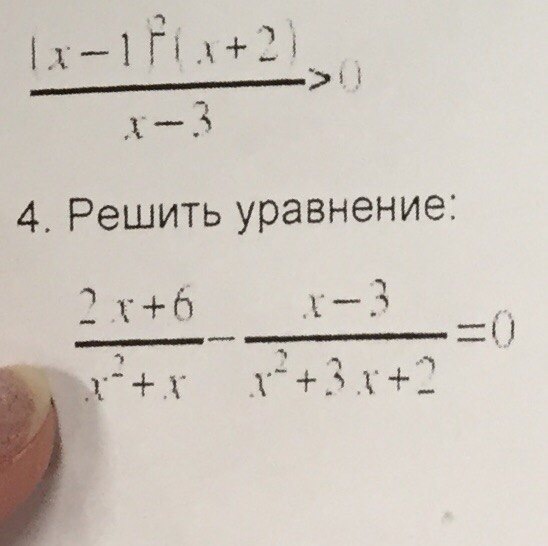
Ответы
Автор ответа:
0
найдем одз:

разложим x^2+3x+2 на множители по корням(мы их уже нашли, когда определяли одз)
x^2+3x+2=(x+2)(x+1)
получим:

корни x1 и x2 не подходят по одз.
В итоге уравнение имеет только 1 корень: x=-12
Ответ: x=-12
разложим x^2+3x+2 на множители по корням(мы их уже нашли, когда определяли одз)
x^2+3x+2=(x+2)(x+1)
получим:
корни x1 и x2 не подходят по одз.
В итоге уравнение имеет только 1 корень: x=-12
Ответ: x=-12
Похожие вопросы
Предмет: Алгебра,
автор: drawnok123
Предмет: Физика,
автор: pineappleindress
Предмет: Математика,
автор: maha1999bek
Предмет: Алгебра,
автор: Coronos1