Question

Помогите♥
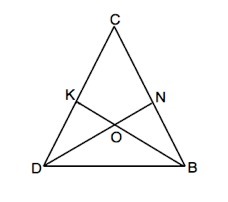
Медианы BK и DN равностороннего треугольника DCB пересекаются в точке O. Докажите, что треугольник BON = треугольнику DOK.

Answer 1

Медианы треугольника пересекаются в одной точке и делятся этой точкой в отношении 2:1, считая от вершины. 

ВО:ОК=2:1

SO:ON=2:1

В равностороннем треугольнике медианы равны. Следовательно, равны и их сходственные отрезки. 

В ∆ DOK  и ∆ BON равны две стороны и углы между ними при вершине О  как вертикальные. Следовательно, эти треугольники равны по первому признаку.  

--------

∆ DOK  и ∆ BON равны и по 3-му признаку, т.к. у равных сторон равны и их половины. 

А, поскольку медианы являются здесь и биссектрисами и высотами, то можно доказать их равенство и по второму признаку.