Предмет: Математика,
автор: BortichS1
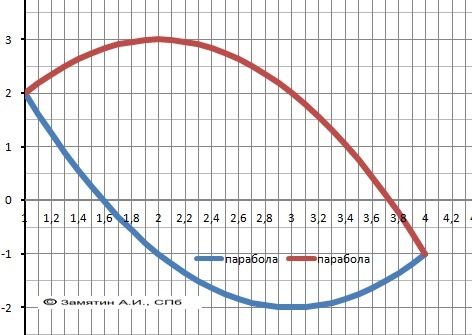
Вычислить площадь фигуры,ограниченной линиями y=x^2-6x+7, y=-x^2+4x-1.Сделать чертеж
Ответы
Автор ответа:
0
РЕШЕНИЕ
Сразу рисунок к задаче в приложении.
Площадь фигуры - интеграл разности функций ограничивающих её.
Находим пределы интегрирования решив уравнение.
x²-6x+7= -x²+4x-1
Упрощаем
2*x² -2x+8 = 0
Решаем квадратное уравнение и находим корни.
Пределы интегрирования - a = 4, b = 1.
Находим разность функций.
Y = -x²+4x-1 - (x²-6x+7) = -8 +10*x - 2x²
Находим интеграл разности функций

ОТВЕТ: Площадь = 9.
Сразу рисунок к задаче в приложении.
Площадь фигуры - интеграл разности функций ограничивающих её.
Находим пределы интегрирования решив уравнение.
x²-6x+7= -x²+4x-1
Упрощаем
2*x² -2x+8 = 0
Решаем квадратное уравнение и находим корни.
Пределы интегрирования - a = 4, b = 1.
Находим разность функций.
Y = -x²+4x-1 - (x²-6x+7) = -8 +10*x - 2x²
Находим интеграл разности функций
ОТВЕТ: Площадь = 9.
Приложения:
Похожие вопросы
Предмет: Математика,
автор: mingaleeva2010
Предмет: Русский язык,
автор: enom83
Предмет: Алгебра,
автор: Аноним
Предмет: Литература,
автор: 3412561