Предмет: Алгебра,
автор: 8Kate567
напишите уравнение касательной к графику функции у= f(x), проведенной в точке N (a;b):
1) f(x)=x
Приложения:
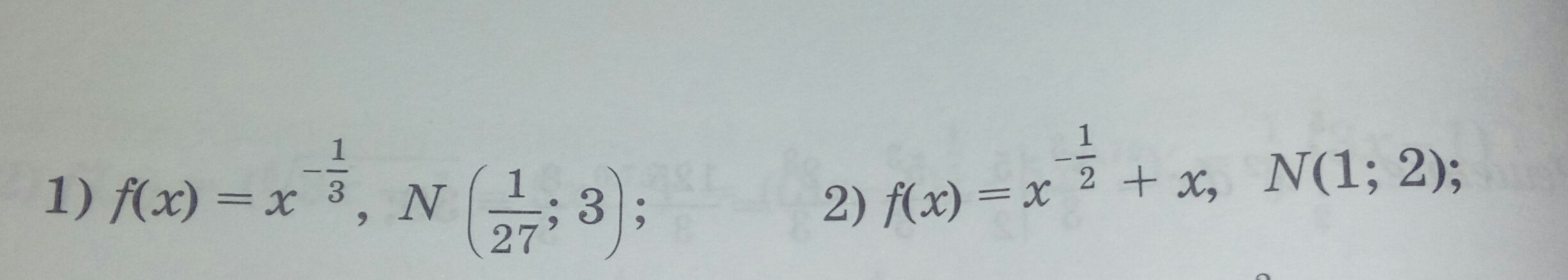
Ответы
Автор ответа:
0
уравнение касательной к графику функции f(x) в точке с абсциссой x0

1)

Ответ: y=4-27x
2)

Ответ: y=0,5x+1,5
1)
Ответ: y=4-27x
2)
Ответ: y=0,5x+1,5
Похожие вопросы
Предмет: Математика,
автор: Bilollol
Предмет: Математика,
автор: kristikrajm6
Предмет: Геометрия,
автор: horkovaana420
Предмет: Математика,
автор: sasha488
Предмет: Алгебра,
автор: kombogame