Предмет: Геометрия,
автор: illay0409
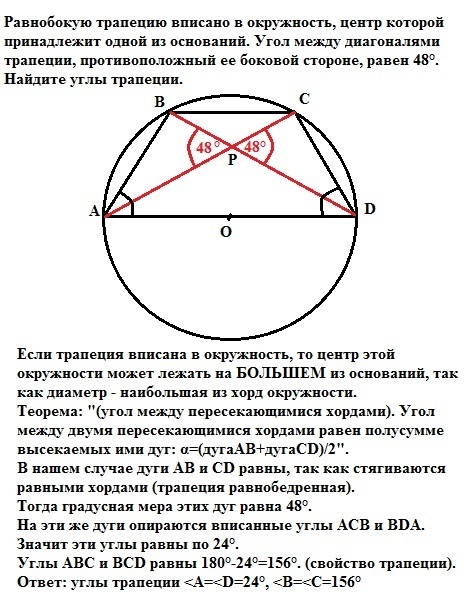
Равнобокую трапецию вписано в окружность, центр которой принадлежит одной из оснований. Угол между диагоналями трапеции, противоположный ее боковой стороне, равен 48°. Найдите углы трапеции.
Ответы
Автор ответа:
0
Если трапеция вписана в окружность, то центр этой окружности может лежать только на БОЛЬШЕМ из оснований, так как диаметр - наибольшая из хорд окружности.
Теорема: "(угол между пересекающимися хордами). Угол между двумя пересекающимися хордами равен полусумме высекаемых ими дуг: α=(дугаАВ+дугаCD)/2".
В нашем случае пересекающиеся хорды - это диагонали трапеции.
Дуги АВ и CD равны, так как стягиваются равными хордами (трапеция равнобедренная).
Тогда градусная мера этих дуг равна 48°.
На эти же дуги опираются вписанные углы АСВ и ВDA.
Значит эти углы равны по 24°.
Углы АВС и ВСD равны 180°-24°=156°. (свойство трапеции).
Ответ: углы трапеции <A=<D=24°, <B=<C=156°.
Теорема: "(угол между пересекающимися хордами). Угол между двумя пересекающимися хордами равен полусумме высекаемых ими дуг: α=(дугаАВ+дугаCD)/2".
В нашем случае пересекающиеся хорды - это диагонали трапеции.
Дуги АВ и CD равны, так как стягиваются равными хордами (трапеция равнобедренная).
Тогда градусная мера этих дуг равна 48°.
На эти же дуги опираются вписанные углы АСВ и ВDA.
Значит эти углы равны по 24°.
Углы АВС и ВСD равны 180°-24°=156°. (свойство трапеции).
Ответ: углы трапеции <A=<D=24°, <B=<C=156°.
Приложения:
Похожие вопросы
Предмет: Оʻzbek tili,
автор: maryamiya12
Предмет: Русский язык,
автор: kristinanice2004
Предмет: Геометрия,
автор: viktae3012
Предмет: Алгебра,
автор: Аноним